In teoria della misura , il teorema di Carathéodory permette di ricavare uno spazio di misura quando si ha a disposizione una misura esterna .
Ad esempio, la misura di Lebesgue in
R
n
{\displaystyle \mathbb {R} ^{n}}
misura esterna
λ
∗
{\displaystyle \lambda ^{*}}
A
⊂
R
n
{\displaystyle A\subset \mathbb {R} ^{n}}
[ 1]
A
{\displaystyle A}
Carathéodory fornisce una σ-algebra di sottoinsiemi di
R
n
{\displaystyle \mathbb {R} ^{n}}
λ
∗
{\displaystyle \lambda ^{*}}
teorema di Hahn-Kolmogorov [ 2]
Sia
X
{\displaystyle X}
insieme e
μ
∗
:
P
(
X
)
→
[
0
,
+
∞
]
{\displaystyle \mu ^{*}\colon {\mathcal {P}}(X)\to [0,+\infty ]}
P
(
X
)
{\displaystyle {\mathcal {P}}(X)}
insieme delle parti di
X
{\displaystyle X}
funzione tale che
μ
∗
(
∅
)
=
0
{\displaystyle \mu ^{*}(\varnothing )=0}
M
:=
{
A
∈
P
(
X
)
:
∀
E
⊂
X
μ
∗
(
E
)
=
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
)
}
{\displaystyle {\mathcal {M}}:=\{A\in {\mathcal {P}}(X):\forall E\subset X\quad \mu ^{*}(E)=\mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c})\}}
è un'algebra e
μ
{\displaystyle \mu }
μ
∗
{\displaystyle \mu ^{*}}
M
{\displaystyle {\mathcal {M}}}
additiva .
Inoltre, se
μ
∗
{\displaystyle \mu ^{*}}
misura esterna , cioè gode anche della monotonia e della subadditività numerabile, allora
M
{\displaystyle {\mathcal {M}}}
σ-algebra e
μ
{\displaystyle \mu }
misura completa .
Si sottolinea che il teorema vale indipendentemente da come viene costruita nella pratica
μ
∗
{\displaystyle \mu ^{*}}
La dimostrazione usa tecniche di routine in teoria della misura e si compone di cinque parti. Nelle prime due si dimostra che
M
{\displaystyle {\mathcal {M}}}
μ
{\displaystyle \mu }
additiva . Nella terza e nella quarta, sotto l'ipotesi aggiuntiva che
μ
∗
{\displaystyle \mu ^{*}}
misura esterna , si vede che in effetti vale di più, cioè che
M
{\displaystyle {\mathcal {M}}}
unioni numerabili e che
μ
{\displaystyle \mu }
σ-additiva , cioè
M
{\displaystyle {\mathcal {M}}}
σ-algebra e
μ
{\displaystyle \mu }
misura . Infine si controlla che
μ
{\displaystyle \mu }
completa .
Per alleggerire la scrittura diremo che
A
⊂
X
{\displaystyle A\subset X}
spezza
E
⊂
X
{\displaystyle E\subset X}
μ
∗
(
E
)
=
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
)
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c})}
quindi
A
∈
M
{\displaystyle A\in {\mathcal {M}}}
X
{\displaystyle X}
L'insieme vuoto spezza tutti i sottoinsiemi perché
μ
∗
(
∅
)
=
0
{\displaystyle \mu ^{*}(\varnothing )=0}
μ
∗
(
E
∩
∅
)
+
μ
∗
(
E
∩
X
)
=
μ
∗
(
∅
)
+
μ
∗
(
E
)
=
μ
∗
(
E
)
{\displaystyle \mu ^{*}(E\cap \varnothing )+\mu ^{*}(E\cap X)=\mu ^{*}(\varnothing )+\mu ^{*}(E)=\mu ^{*}(E)}
qualsiasi sia
E
⊂
X
{\displaystyle E\subset X}
La proprietà di spezzare un sottoinsieme è simmetrica rispetto al complementare , cioè se
A
{\displaystyle A}
E
{\displaystyle E}
A
c
{\displaystyle A^{c}}
E
{\displaystyle E}
M
{\displaystyle {\mathcal {M}}}
Siano
A
,
B
∈
M
{\displaystyle A,B\in {\mathcal {M}}}
E
⊂
X
{\displaystyle E\subset X}
E
{\displaystyle E}
A
{\displaystyle A}
μ
∗
(
E
)
=
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
)
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c})}
e poi con B l'insieme relativo al secondo termine
μ
∗
(
E
)
=
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
∩
B
)
+
μ
∗
(
E
∩
A
c
∩
B
c
)
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c}\cap B)+\mu ^{*}(E\cap A^{c}\cap B^{c})}
ora si noti che
E
∩
A
=
E
∩
(
A
∪
B
)
∩
A
{\displaystyle E\cap A=E\cap (A\cup B)\cap A}
E
∩
A
c
∩
B
=
E
∩
(
A
∪
B
)
∩
A
c
{\displaystyle E\cap A^{c}\cap B=E\cap (A\cup B)\cap A^{c}}
proprietà distributiva dell'intersezione rispetto all'unione), quindi spezzando con
A
{\displaystyle A}
E
∩
(
A
∪
B
)
{\displaystyle E\cap (A\cup B)}
μ
∗
(
E
∩
(
A
∪
B
)
)
=
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
∩
B
)
,
{\displaystyle \mu ^{*}(E\cap (A\cup B))=\mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c}\cap B),}
cioè (per le leggi di De Morgan )
μ
∗
(
E
)
=
μ
∗
(
E
∩
(
A
∪
B
)
)
+
μ
∗
(
E
∩
A
c
∩
B
c
)
=
μ
∗
(
E
∩
(
A
∪
B
)
)
+
μ
∗
(
E
∩
(
A
∪
B
)
c
)
.
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap (A\cup B))+\mu ^{*}(E\cap A^{c}\cap B^{c})=\mu ^{*}(E\cap (A\cup B))+\mu ^{*}(E\cap (A\cup B)^{c}).}
In altre parole
A
∪
B
{\displaystyle A\cup B}
X
{\displaystyle X}
M
{\displaystyle {\mathcal {M}}}
La verifica è facile. Siano
A
,
B
∈
M
{\displaystyle A,B\in {\mathcal {M}}}
disgiunti , quindi
B
⊂
A
c
{\displaystyle B\subset A^{c}}
A
∪
B
{\displaystyle A\cup B}
A
{\displaystyle A}
μ
∗
(
A
∪
B
)
=
μ
∗
(
(
A
∪
B
)
∩
A
)
+
μ
∗
(
(
A
∪
B
)
∩
A
c
)
=
μ
∗
(
A
)
+
μ
∗
(
B
)
.
{\displaystyle \mu ^{*}(A\cup B)=\mu ^{*}((A\cup B)\cap A)+\mu ^{*}((A\cup B)\cap A^{c})=\mu ^{*}(A)+\mu ^{*}(B).}
Da qui in poi si assume che
μ
∗
{\displaystyle \mu ^{*}}
misura esterna .
Si ricorda che una σ-algebra è un'algebra chiusa rispetto alle unioni numerabili.
Sia
{
C
n
}
n
∈
N
{\displaystyle \{C_{n}\}_{n\in \mathbb {N} }}
famiglia numerabile di elementi di
M
{\displaystyle {\mathcal {M}}}
E
⊂
X
{\displaystyle E\subset X}
n
∈
N
{\displaystyle n\in \mathbb {N} }
A
n
:=
C
n
−
C
1
−
…
−
C
n
−
1
.
{\displaystyle A_{n}:=C_{n}-C_{1}-\dots {}-C_{n-1}.}
Si ottiene così una famiglia
{
A
n
}
{\displaystyle \{A_{n}\}}
B
n
:=
⋃
k
=
1
n
A
k
{\displaystyle B_{n}:=\bigcup _{k=1}^{n}A_{k}\qquad }
B
:=
⋃
n
=
1
+
∞
A
n
.
{\displaystyle \qquad B:=\bigcup _{n=1}^{+\infty }A_{n}.}
Si vuole dimostrare che
B
{\displaystyle B}
E
{\displaystyle E}
M
{\displaystyle {\mathcal {M}}}
B
n
{\displaystyle B_{n}}
E
{\displaystyle E}
Spezzando
E
{\displaystyle E}
B
n
{\displaystyle B_{n}}
μ
∗
(
E
)
=
μ
∗
(
E
∩
B
n
)
+
μ
∗
(
E
∩
B
n
c
)
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap B_{n})+\mu ^{*}(E\cap B_{n}^{c})}
si noti che
B
n
⊂
B
{\displaystyle B_{n}\subset B}
B
c
⊂
B
n
c
{\displaystyle B^{c}\subset B_{n}^{c}}
monotonia di
μ
∗
{\displaystyle \mu ^{*}}
μ
∗
(
E
)
≥
μ
∗
(
E
∩
B
n
)
+
μ
∗
(
E
∩
B
c
)
.
{\displaystyle \mu ^{*}(E)\geq \mu ^{*}(E\cap B_{n})+\mu ^{*}(E\cap B^{c}).}
Adesso si lavora su
μ
∗
(
E
∩
B
n
)
{\displaystyle \mu ^{*}(E\cap B_{n})}
n
→
+
∞
{\displaystyle n\to +\infty }
E
∩
B
n
{\displaystyle E\cap B_{n}}
A
n
{\displaystyle A_{n}}
μ
∗
(
E
∩
B
n
)
=
μ
∗
(
E
∩
A
n
)
+
μ
∗
(
E
∩
B
n
−
1
)
{\displaystyle \mu ^{*}(E\cap B_{n})=\mu ^{*}(E\cap A_{n})+\mu ^{*}(E\cap B_{n-1})}
e procedendo per induzione
μ
∗
(
E
∩
B
n
)
=
∑
k
=
1
n
μ
∗
(
E
∩
A
k
)
.
{\displaystyle \mu ^{*}(E\cap B_{n})=\sum _{k=1}^{n}\mu ^{*}(E\cap A_{k}).}
Quindi
μ
∗
(
E
)
≥
∑
k
=
1
n
μ
∗
(
E
∩
A
n
)
+
μ
∗
(
E
∩
B
c
)
{\displaystyle \mu ^{*}(E)\geq \sum _{k=1}^{n}\mu ^{*}(E\cap A_{n})+\mu ^{*}(E\cap B^{c})}
e passando al limite per
n
→
+
∞
{\displaystyle n\to +\infty }
μ
∗
(
E
)
≥
∑
k
=
1
+
∞
μ
∗
(
E
∩
A
k
)
+
μ
∗
(
E
∩
B
c
)
.
{\displaystyle \mu ^{*}(E)\geq \sum _{k=1}^{+\infty }\mu ^{*}(E\cap A_{k})+\mu ^{*}(E\cap B^{c}).}
Usando la subadditività numerabile di
μ
∗
{\displaystyle \mu ^{*}}
∑
n
=
1
+
∞
μ
∗
(
E
∩
A
k
)
≥
μ
∗
(
⋃
k
=
1
+
∞
(
E
∩
A
k
)
)
=
μ
∗
(
E
∩
B
)
{\displaystyle \sum _{n=1}^{+\infty }\mu ^{*}(E\cap A_{k})\geq \mu ^{*}\left(\bigcup _{k=1}^{+\infty }(E\cap A_{k})\right)=\mu ^{*}(E\cap B)}
e quindi che
μ
∗
(
E
)
≥
μ
∗
(
E
∩
B
)
+
μ
∗
(
E
∩
B
c
)
≥
μ
∗
(
(
E
∩
B
)
∪
(
E
∩
B
c
)
)
=
μ
∗
(
E
)
{\displaystyle \mu ^{*}(E)\geq \mu ^{*}(E\cap B)+\mu ^{*}(E\cap B^{c})\geq \mu ^{*}((E\cap B)\cup (E\cap B^{c}))=\mu ^{*}(E)}
cioè
μ
∗
(
E
)
=
μ
∗
(
E
∩
B
)
+
μ
∗
(
E
∩
B
c
)
.
{\displaystyle \mu ^{*}(E)=\mu ^{*}(E\cap B)+\mu ^{*}(E\cap B^{c}).}
Si ricorda che una misura su una σ-algebra è un funzione a valori reali positivi σ-additiva che assegna 0 all'insieme vuoto. Anche la verifica della σ-additività di
μ
∗
{\displaystyle \mu ^{*}}
M
{\displaystyle {\mathcal {M}}}
Sia
{
A
n
}
n
∈
N
{\displaystyle \{A_{n}\}_{n\in \mathbb {N} }}
M
{\displaystyle {\mathcal {M}}}
B
=
⋃
n
=
1
+
∞
A
n
.
{\displaystyle B=\bigcup _{n=1}^{+\infty }A_{n}.}
Dall'additività e dalla monotonia di
μ
∗
{\displaystyle \mu ^{*}}
μ
∗
(
A
1
)
+
μ
∗
(
A
2
)
+
…
+
μ
∗
(
A
n
)
=
μ
∗
(
A
1
∪
A
2
∪
…
∪
A
n
)
≤
μ
∗
(
B
)
,
{\displaystyle \mu ^{*}(A_{1})+\mu ^{*}(A_{2})+\ldots {}+\mu ^{*}(A_{n})=\mu ^{*}(A_{1}\cup A_{2}\cup \ldots {}\cup A_{n})\leq \mu ^{*}(B),}
questo vale per tutti gli
n
{\displaystyle n}
n
→
+
∞
{\displaystyle n\to +\infty }
∑
n
=
1
+
∞
μ
∗
(
A
n
)
≤
μ
∗
(
B
)
.
{\displaystyle \sum _{n=1}^{+\infty }\mu ^{*}(A_{n})\leq \mu ^{*}(B).}
La subadditività numerabile di
μ
∗
{\displaystyle \mu ^{*}}
μ
∗
(
B
)
=
∑
n
=
1
+
∞
μ
∗
(
A
n
)
.
{\displaystyle \mu ^{*}(B)=\sum _{n=1}^{+\infty }\mu ^{*}(A_{n}).}
Si ricorda che completa significa che se
Z
∈
M
{\displaystyle Z\in {\mathcal {M}}}
A
⊂
Z
{\displaystyle A\subset Z}
μ
(
Z
)
=
0
{\displaystyle \mu (Z)=0}
A
∈
M
{\displaystyle A\in {\mathcal {M}}}
Dimostriamo prima che se
A
⊂
X
{\displaystyle A\subset X}
μ
∗
(
A
)
=
0
{\displaystyle \mu ^{*}(A)=0}
A
∈
M
{\displaystyle A\in {\mathcal {M}}}
Sia
E
⊂
X
{\displaystyle E\subset X}
μ
∗
(
E
)
=
μ
∗
(
(
E
∩
A
)
∪
(
E
∩
A
c
)
)
≤
μ
∗
(
E
∩
A
)
+
μ
∗
(
E
∩
A
c
)
≤
μ
∗
(
A
)
+
μ
∗
(
E
)
=
μ
∗
(
E
)
.
{\displaystyle \mu ^{*}(E)=\mu ^{*}((E\cap A)\cup (E\cap A^{c}))\leq \mu ^{*}(E\cap A)+\mu ^{*}(E\cap A^{c})\leq \mu ^{*}(A)+\mu ^{*}(E)=\mu ^{*}(E).}
Ora se
A
⊂
Z
{\displaystyle A\subset Z}
Z
∈
M
{\displaystyle Z\in {\mathcal {M}}}
μ
∗
(
Z
)
=
0
{\displaystyle \mu ^{*}(Z)=0}
μ
∗
(
A
)
=
0
{\displaystyle \mu ^{*}(A)=0}
A
∈
M
{\displaystyle A\in {\mathcal {M}}}
Si ricorda che se
μ
0
:
A
→
[
0
,
+
∞
]
{\displaystyle \mu _{0}\colon {\mathcal {A}}\to [0,+\infty ]}
A
⊂
P
(
X
)
{\displaystyle {\mathcal {A}}\subset {\mathcal {P}}(X)}
∅
,
X
∈
A
{\displaystyle \varnothing ,X\in {\mathcal {A}}}
μ
0
(
∅
)
=
0
{\displaystyle \mu _{0}(\varnothing )=0}
μ
0
{\displaystyle \mu _{0}}
Metodo I
μ
∗
:
P
(
X
)
→
[
0
,
+
∞
]
{\displaystyle \mu ^{*}\colon {\mathcal {P}}(X)\to [0,+\infty ]}
μ
∗
(
E
)
:=
inf
{
∑
k
=
1
+
∞
μ
0
(
A
k
)
:
{
A
k
}
k
∈
N
⊂
A
,
E
⊂
⋃
k
=
1
+
∞
A
k
}
{\displaystyle \mu ^{*}(E):=\inf \left\{\sum _{k=1}^{+\infty }\mu _{0}(A_{k}):\{A_{k}\}_{k\in \mathbb {N} }\subset {\mathcal {A}},\;E\subset \bigcup _{k=1}^{+\infty }A_{k}\right\}}
si può verificare[ 3] misura esterna .
Si ricorda inoltre che se
A
{\displaystyle {\mathcal {A}}}
μ
0
:
A
→
[
0
,
+
∞
]
{\displaystyle \mu _{0}\colon {\mathcal {A}}\to [0,+\infty ]}
premisura (o semplicemente misura, basta non confondersi) se per ogni famiglia numerabile
{
A
k
}
k
∈
N
⊂
A
,
∀
i
,
j
∈
N
i
≠
j
A
k
∩
A
j
=
∅
{\displaystyle \{A_{k}\}_{k\in \mathbb {N} }\subset {\mathcal {A}},\;\;\forall i,j\in \mathbb {N} \;\;i\neq j\;\;A_{k}\cap A_{j}=\varnothing }
A
{\displaystyle {\mathcal {A}}}
μ
0
(
⋃
k
=
1
+
∞
A
k
)
=
∑
k
=
1
+
∞
μ
0
(
A
k
)
.
{\displaystyle \mu _{0}\left(\bigcup _{k=1}^{+\infty }A_{k}\right)=\sum _{k=1}^{+\infty }\mu _{0}(A_{k}).}
Nel caso in cui
μ
∗
{\displaystyle \mu ^{*}}
Metodo I
μ
0
{\displaystyle \mu _{0}}
A
{\displaystyle {\mathcal {A}}}
(
X
,
M
,
μ
)
{\displaystyle (X,{\mathcal {M}},\mu )}
tutti gli elementi di
A
{\displaystyle {\mathcal {A}}}
A
⊂
M
{\displaystyle {\mathcal {A}}\subset {\mathcal {M}}}
A
{\displaystyle {\mathcal {A}}}
M
{\displaystyle {\mathcal {M}}}
la misura
μ
{\displaystyle \mu }
A
{\displaystyle {\mathcal {A}}}
μ
0
{\displaystyle \mu _{0}}
se
X
{\displaystyle X}
A
{\displaystyle {\mathcal {A}}}
μ
{\displaystyle \mu }
A
{\displaystyle {\mathcal {A}}}
μ
0
{\displaystyle \mu _{0}}
Talvolta in letteratura queste tre affermazioni vanno sotto il nome di teorema di Hahn-Kolmogorov [ 4]
^ unioni finite di parallelepipedi con i lati paralleli agli assi coordinati
^ questo non è propriamente vero, nel senso che prima di poter usare il teorema bisogna dimostrare che l'insieme di tutti i pluri-parallelepipedi costituisce un'algebra e che il volume è una premisura su di essa. Resta comunque il fatto che viene risparmiato il grosso del lavoro, cioè l'estensione alla σ-algebra generata.
^ Folland , Proposizione 1.10 p. 29^ o teorema di Hahn, o teorema di Kolmogorov, o spesso non viene neanche assegnato un nome, dipende dalle simpatie dell'autore. Ad esempio in Lang , Teorema 7.1 p. 153 viene chiamato teorema di Hahn.
(EN Measure theory, volume 1 , Springer, 2006, ISBN 3-540-34513-2 . (EN Gerald Folland , Real Analysis: Modern Techniques and Their Applications ISBN 0-471-31716-0 . (EN Real and Functional Analysis , Springer, 1993, ISBN 0-387-94001-4 . 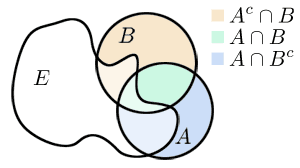














![{\displaystyle \mu ^{*}\colon {\mathcal {P}}(X)\to [0,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2158fa7757a8790b23cd3fe4b5f477cca20b12a2)


























































![{\displaystyle \mu _{0}\colon {\mathcal {A}}\to [0,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08dd5f9921453f74a011d778758c4fdf00525895)










