Indice
Rosa (topologia)
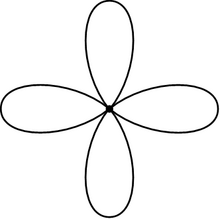
In matematica, una rosa (nota anche come bouquet o mazzo di n cerchi) è uno spazio topologico ottenuto incollando un insieme di ipersfere (o, in due dimensioni, cerchi) con un unico punto in comune. I cerchi della rosa si chiamano petali. Le rose sono importanti nella topologia algebrica, dove sono strettamente correlate ai gruppi liberi.
Definizione
[modifica | modifica wikitesto]
Una rosa è un bouquet di ipersfere (o cerchi bidimensionali). In altre parole, la rosa è lo spazio quoziente dove è un'unione disgiunta di cerchi e un insieme costituito da un punto per ciascun cerchio. Essendo un complesso di celle, una rosa ha un singolo vertice e un bordo per ciascun cerchio. Questo lo rende un semplice esempio di grafo topologico.
Una rosa con n petali si può ottenere anche individuando n punti su un unico cerchio. La rosa con due petali è conosciuta come figura otto.
Relazione con i gruppi liberi
[modifica | modifica wikitesto]
Il gruppo fondamentale di una rosa è libero, con un generatore per ogni petalo. La copertura universale è un albero infinito, identificabile con il grafo di Cayley del gruppo libero. Questo è un caso speciale del complesso di presentazione associato a qualsiasi presentazione di un gruppo.
Le coperture intermedie della rosa corrispondono ai sottogruppi del gruppo libero. L’osservazione che ogni copertura di una rosa è un grafo fornisce una semplice prova che ogni sottogruppo di un gruppo libero è libero (teorema di Nielsen-Schreier)
Poiché la copertura universale di una rosa è contraibile, la rosa è in realtà uno spazio di Eilenberg-MacLane per il gruppo libero associato . Ciò implica che i gruppi di coomologia sono banali per .
Altre proprietà
[modifica | modifica wikitesto]
- Qualsiasi grafo connesso è omotopicamente equivalente a una rosa. Nello specifico, la rosa è lo spazio quoziente del grafo ottenuto facendo collassare un albero ricoprente.
- Una palla con n punti rimossi (o una sfera con punti rimossi) si ritrae per deformazione su una rosa con n petali. Un petalo della rosa circonda ciascuno dei punti rimossi.
- Un toro con un punto rimosso si ritrae per deformazione in una figura otto, cioè l'unione di due cerchi generatori. Più in generale, una superficie del genere g a cui è stato rimosso un punto si ritrae per deformazione su una rosa con 2 petali g, cioè il confine di un poligono fondamentale.
- Una rosa può avere infiniti petali, dando origine ad un gruppo fondamentale che è libero su infiniti generatori. La rosa con infiniti petali numerabili è simile all'orecchino hawaiano: c'è una biiezione continua da questa rosa all'orecchino hawaiano, ma i due non sono omeomorfi. Una rosa con infiniti petali non è compatta, mentre l’orecchino hawaiano è compatto.
Bibliografia
[modifica | modifica wikitesto]- Allen Hatcher, Algebraic topology, Cambridge university press, 2001, ISBN 978-0-521-79540-1.
- James Raymond Munkres, Topology, 2nd ed, Prentice Hall, 2000, ISBN 978-0-13-181629-9.
- John Stillwell, Classical topology and combinatorial group theory, collana Graduate texts in mathematics, 2nd ed, Springer-Verlag, 1995, ISBN 978-0-387-97970-0.

















