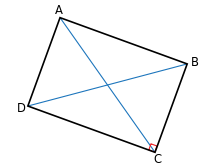
In geometria, il rettangolo è un parallelogramma che ha tutti gli angoli interni congruenti tra loro (e, di conseguenza, retti).

Da questa definizione si evince che in un rettangolo ciascuna delle due coppie di lati opposti è costituita da lati congruenti; in altre parole i rettangoli sono particolari parallelogrammi. I rettangoli sono anche particolari quadrilateri ciclici: si possono definire come i quadrilateri ciclici aventi come diagonali due diametri del cerchio circoscritto.

Il quadrato è un tipo particolare di rettangolo, caratterizzato dall'avere tutti i quattro lati congruenti. Equivalentemente si dice che l'insieme dei quadrati è l'intersezione dell'insieme dei rettangoli con l'insieme dei rombi.

Nel parlare colloquiale per sottolineare che un rettangolo non ha tutti i lati congruenti come un quadrato, si dice che un rettangolo è una figura oblunga. Quando si presenta un rettangolo nel piano cartesiano e questo ha due lati sensibilmente più lunghi degli altri due e disposti orizzontalmente, si parla di rettangolo largo; se invece i lati più lunghi sono disposti verticalmente si parla di rettangolo alto o addirittura di rettangolo sottile. La lunghezza dei due lati opposti più lunghi viene chiamata lunghezza o base del rettangolo, mentre la lunghezza dei due lati più corti viene chiamata larghezza o altezza.

Un quadrilatero convesso è un rettangolo se e solo se possiede una di queste caratteristiche equivalenti:^[1][2]

• un parallelogramma con almeno un angolo retto;
• un parallelogramma equiangolo;
• un parallelogramma con le diagonali di pari lunghezza;
• un parallelogramma ABCD dove i triangoli ABD e DCA sono congruenti;
• un quadrilatero che ha quattro angoli retti;
• un quadrilatero equiangolo.

Il poligono duale del rettangolo è un rombo, come illustrato nella tabella sottostante.^[3]

L'area del rettangolo è il prodotto della sua lunghezza per la sua larghezza, ovvero della sua base per la sua altezza. Per esempio, il rettangolo nella prima figura ha una base di 5 u e un'altezza di 4 u: la sua area è quindi 20 u², risultato della moltiplicazione 5 × 4.

Se invece la base e l'altezza di un rettangolo si indicano rispettivamente con ${\displaystyle \,b}$ ed ${\displaystyle \,h}$ per la sua area ${\displaystyle \,A}$ e per il suo perimetro ${\displaystyle \,2p}$ si ha:

• Area ${\displaystyle A\,=\,b\cdot h}$
• Perimetro ${\displaystyle 2p\,=\,2\cdot b+2\cdot h\,=\,2\cdot (b+h)}$
• Diagonale ${\displaystyle d={\sqrt {b^{2}+h^{2}}}}$ (teorema di Pitagora)

Nel calcolo infinitesimale l'integrale di Riemann viene definito come limite delle somme delle aree di rettangoli via via più sottili.

Il termine, inteso come aggettivo, può specificare altre figure geometriche.

• Triangolo rettangolo è un triangolo avente un angolo retto.
• Trapezio rettangolo è un trapezio nel quale i due angoli adiacenti a un lato obliquo sono retti.
• Prisma retto è un prisma avente le facce laterali perpendicolari alle basi
• Piramide retta è una piramide avente il vertice allineato con il centro della base

• Iperrettangolo
• Quadrato
• Quadrilatero
• Rombo (geometria)

• Wikizionario contiene il lemma di dizionario «rettangolo»
• Wikimedia Commons contiene immagini o altri file su rettangolo

• (EN) Eric W. Weisstein, Rettangolo, su MathWorld, Wolfram Research.

V · D · M Poligoni
Poligoni per numero di lati	Triangolo (3) · Quadrilatero (4) · Pentagono (5) · Esagono (6) · Ettagono (7) · Ottagono (8) · Ennagono (9) · Decagono (10) · Endecagono (11) · Dodecagono (12) · Tridecagono (13) · Tetradecagono (14) · Pentadecagono (15) · Esadecagono (16) · Eptadecagono (17) · Ottadecagono (18) · Ennadecagono (19) · Icosagono (20) · Endeicosagono (21) · Doicosagono (22) · Triacontagono (30) · Pentacontagono (50) · 257-gono (257) · Chiliagono (1 000) · Miriagono (10 000) · 65537-gono (65 537)
Triangoli	In base ai lati: Triangolo equilatero · Triangolo isoscele · Triangolo scaleno · In base agli angoli: Triangolo rettangolo · Triangolo acutangolo · Triangolo ottusangolo
Quadrilateri	Quadrato · Rettangolo · Parallelogramma · Rombo · Trapezio · Aquilone
Poligoni stellati	Pentagramma · Esagramma · Eptagramma · Ottagramma · Enneagramma · Decagramma · Endecagramma · Dodecagramma
Altri	Poligono regolare · Poligono equilatero · Poligono equiangolo · Poligono sghembo

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica