Indice
Poligono sghembo

In geometria descrittiva, un poligono sghembo è un poligono (ossia un 2-politopo) i cui vertici non sono tutti complanari.[1] La superficie di tali poligoni, che devono avere almeno quattro vertici, non è definita in modo univoco.
Un particolare tipo di poligoni sghembi, detti poligoni antiprismatici o poligoni sghembi a zig-zag, che include poi tutti i poligoni sghembi regolari tridimensionali nonché gli apeirogoni sghembi regolari bidimensionali, ha i vertici che si alternano su due piani paralleli ed ha quindi sempre un numero pari di vertici.
Poligoni antiprismatici in tre dimensioni
[modifica | modifica wikitesto]Un poligono sghembo regolare è una figura isogonale equilatera. In uno spazio tridimensionale tale poligono è un poligono sghembo a zig-zag (o antiprismatico), con vertici alternati tra due piani paralleli. Gli spigoli laterali di un antiprisma n-gonale possono ad esempio definire un 2n-gono sghembo regolare.[2]
A un n-gono sghembo regolare può essere assegnato un simbolo di Schläfli {p}#{ } dato dalla combinazione del simbolo di un poligono regolare {p} e quello di un segmento ortogonale { }.
Nella tabella sottostante sono mostrati esempi relativi ad antriprismi quadrati e pentagonali uniformi. Si noti come gli antiprismi stellati possano generare anche poligoni sghembi regolari aventi un diverso ordine di connessione tra i poligoni superiore ed inferiore. Si noti inoltre che questi ultimi due vengono rappresentati colorati solo per chiarezza e non per indicare una loro appartenenza ai poligoni sghembi.
| Quadrato sghembo | Esagono sghembo | Ottagono sghembo | Decagono sghembo | Dodecagono sghembo | ||
| {2}#{ } | {3}#{ } | {4}#{ } | {5}#{ } | {5/2}#{ } | {5/3}#{ } | {6}#{ } |

|
|

|

|

|

|
|
| s{2,4} | s{2,6} | s{2,8} | s{2,10} | sr{2,5/2} | s{2,10/3} | s{2,12} |
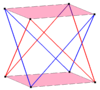
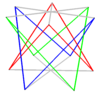
Allo stesso modo si può realizzare un composto 2n-gonale sghembo aggiungendo un secondo poligono sghembo per rotazione. In tal caso le due figure condividono gli stessi vertici come in un composto prismatico di antiprismi.
| Quadrati sghembi | Esagoni sghembi | Decagoni sghembi | |
| Due {2}#{ } | Tre {2}#{ } | Due {3}#{ } | Due {5/3}#{ } |
|
|

|

|
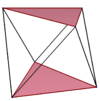
I poligoni di Petrie sono poligoni sghembi regolari definiti all'interno di poliedri e politopi regolari. Ad esempio, come si vede nelle figure sottostanti in cui le proiezioni ortogonali dei poligoni sghembi sono evidenziate di rosso, i cinque solidi platonici contengono poligoni sghembi regolari di 4, 6 e 10 lati. In particolare, poi, il tetraedro e l'ottaedro includono tutti i loro vertici nei rispettivi poligoni sghembi a zig-zag e possono essere visti rispettivamente come un antiprisma digonale e un antiprisma triangolare.[3]
Poligoni sghembi regolari come figure al vertice di poliedri sghembi regolari
[modifica | modifica wikitesto]Un poliedro sghembo regolare è definito come un poliedro avente per facce un poligono regolare e come figura al vertice un poligono sghembo regolare.
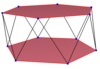
Come mostrato nella sottostante tabella, nello spazio tridimensionale esistono tre poliedri sghembi regolari in grado di tassellare perfettamente lo spazio, vale a dire tre apeiroedri sghembi regolari.
| {4,6|4} | {6,4|4} | {6,6|3} |
|---|---|---|
 Esagono sghembo regolare {3}#{ } |
 Quadrato sghembo regolare {2}#{ } |
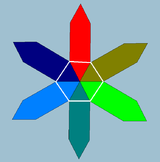 Esagono sghembo regolare {3}#{ } |
Poligoni sghembi isogonali in tre dimensioni
[modifica | modifica wikitesto]Un poligono sghembo isogonale è un poligono sghembo avente un unico tipo di vertici e connesso da due tipi di lati. Qualora i lati di tale poligono siano di pari lunghezza, allora esso può essere considerato quasi-regolare. Si tratta di un poligono sghembo simile a un poligono sghembo a zig-zag, ossia avente come quest'ultimo i vertici posti su due piani diversi, in cui però uno o più lati possono connettere vertici posti sullo stesso piano.[2]
Come mostrato nella tabella sottostante, poligoni sghembi isogonali possono essere definiti su prismi n-gonali con n pari, connettendo alternativamente due vertici su uno stesso piano e due vertici posti su piani diversi.
| Ottagono | Dodecagono | Icositetragono | ||||
|---|---|---|---|---|---|---|
 Cubo, diagonale-quadrato |
 Cubo |
 Cubo incrociato |
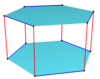 Prisma esagonale |
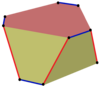 Prisma esagonale |
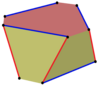 Prisma esagonale |
 Prisma ritorto |
Poligoni sghembi regolari in quattro dimensioni
[modifica | modifica wikitesto]In uno spazio a quattro dimensioni, un poligono sghembo regolare può avere i vertici posti su un toro di Clifford e correlati da rotazioni isocline. Contrariamente ai poligoni sghembi a zig-zag, i poligoni sghembi su rotazioni doppie possono avere anche un numero dispari di lati.
I poligoni di Petrie di policori regolari definiscono poligoni sghembi regolari a zig-zag. Il numero di Coxeter per ogni gruppo di Coxeter indica poi quanti lati tali poligoni di Petrie abbiano; così ad esempio esso è 5 nel caso di un 5-cella (o ipertetraedro), 8 per un tesseratto e un 16-cella (o esadecacoro), 12 per un 24-cella e 30 per un 120-cella e un 600-cella.
| A4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | H4, [5,3,3] | ||
|---|---|---|---|---|---|
| Pentagono | Ottagono | Dodecagono | Triacontagono | ||
 5-cella {3,3,3} |
 tesseratto {4,3,3} |
 16-cella {3,3,4} |
 24-cella {3,4,3} |
 120-cella {5,3,3} |
 600-cella {3,3,5} |
Anche i duoprismi n-n e le duopiramidi loro duali hanno poligoni di Petri 2n-gonali (il tesseratto è di fatto un duoprisma 4-4 e il 16-cella è una duopiramide 4-4.)
| Esagono | Decagono | Dodecagono | |||
|---|---|---|---|---|---|
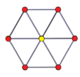 Duoprisma 3-3 |
 Dueopiramide 3-3 |
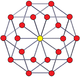 Duoprisma 5-5 |
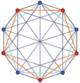 Dueopiramide 5-5 |
 Duoprisma 6-6 |
 Dueopiramide 6-6 |
Note
[modifica | modifica wikitesto]- ^ Luca Goldoni, Complementi sui poligoni (PDF), Università degli Studi di Modena e Reggio Emilia, Dicembre 2015, DOI:10.13140/RG.2.1.3360.6487. URL consultato il 20 aprile 2022.
- ^ a b Harold Scott Macdonald Coxeter, Polygons and Polyhedra, in Regular Polytopes, 3ª ed., New York, Courier Corporation, 1973.
- ^ Harold Scott Macdonald Coxeter, Regular Complex Polytopes, Cambridge University Press, 1991, ISBN 0-521-39490-2.
Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su Poligono sghembo
Wikimedia Commons contiene immagini o altri file su Poligono sghembo
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Eric W. Weisstein, Poligono sghembo, su MathWorld, Wolfram Research.











