Insieme di Julia

In analisi complessa, l'insieme di Julia di una funzione olomorfa consiste di tutti quei punti il cui comportamento dopo ripetute iterazioni della funzione è caotico, nel senso che può cambiare drasticamente in seguito ad una piccola perturbazione iniziale.

Il complementare dell'insieme di Julia nel piano complesso si chiama insieme di Fatou: è l'insieme dei punti il cui comportamento (sempre in seguito a ripetute iterazioni della funzione) è più stabile.

I nomi per questi insiemi si riferiscono ai matematici francesi Gaston Julia e Pierre Fatou, che iniziarono a studiare la dinamica delle funzioni olomorfe all'inizio del XX secolo, considerando il caso delle iterazioni di funzioni razionali.

Consideriamo ad esempio la funzione olomorfa, dipendente da un parametro complesso ${\displaystyle c}$:

${\displaystyle f_{c}(z)=z^{2}+c.}$

L'insieme di tutti i valori ${\displaystyle c}$ per cui l'insieme di Julia di ${\displaystyle f_{c}}$ è connesso forma il celebre insieme di Mandelbrot. Se ${\displaystyle c}$ è fuori di questo insieme, l'insieme di Julia risulta essere omeomorfo all'insieme di Cantor.

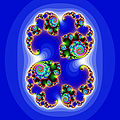
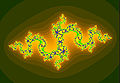
Tramite un calcolatore è possibile rappresentare la dinamica delle iterazioni. Qui di seguito viene rappresentata la dinamica dell'iterazione ${\displaystyle z\rightarrow z^{2}+c}$ per i valori:

${\displaystyle c=\phi -2;\phi -2+(\phi -1)i;0,285.}$

e quindi per:

${\displaystyle c=0,285+0,013i;0,45-0,1428i;-0,70176-0,3842i;-0,835-0,2321i.}$

• (EN) Lennart Carleson and Theodore W. Gamelin, Complex Dynamics, Springer 1993
• (FR) Adrien Douady and John H. Hubbard, Etude dynamique des polynômes complexes, Prépublications mathémathiques d'Orsay 2/4 (1984 / 1985)
• (EN) John Milnor, Dynamics in One Complex Variable (terza edizione), Annals of Mathematics Studies 160, Princeton University Press 2006 (comparso come preprint a Stony Brook nel 1990], disponibile come arXiV:math.DS/9201272.)

• Wikimedia Commons contiene immagini o altri file sull'insieme di Julia

• (EN) Julia set, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Opere riguardanti Julia sets, su Open Library, Internet Archive.
• (EN) Eric W. Weisstein, Julia Set, su MathWorld, Wolfram Research.
• (EN) Julia set, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• Programma in C per creare l'insieme di Julia., su mamo139.altervista.org.
• Un piccolo programma per creare l'insieme di Julia (Windows, 370 kb), su lizardie.com. URL consultato il 29 ottobre 2009 (archiviato dall'url originale il 17 marzo 2011).

V · D · M Teoria del caos
Teoria delle biforcazioni	Biforcazione a forcone · Biforcazione a nodo sella · Biforcazione imperfetta · Biforcazione transcritica · Biforcazione di Hopf · Larva del pino (sistema dinamico)
Frattali	Arte frattale · Buddhabrot · Burning ship · Compressione frattale · Curva di Koch · Curva di Peano · Curva di Sierpiński · Dimensione di Hausdorff · Dimensione frattale · Funzione di Cantor · Insieme di Cantor · Insieme di Julia · Insieme di Mandelbrot · Frattali per dimensione di Hausdorff · Polvere di Cantor · Sterling · Triangolo di Sierpiński · Dimensione di Minkowski-Bouligand
Attrattori	Attrattore di Lorenz · Attrattore di Hénon · Mappa di Poincaré · Mappa logistica · Mappa a ferro di cavallo · Spazio delle fasi
Teorici del caos	Edward Norton Lorenz · Aleksandr Michajlovič Ljapunov · Benoît Mandelbrot · Edward Ott · Henri Poincaré · David Ruelle · Stephen Wolfram · James Yorke

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica