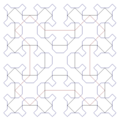
Le curve di Sierpiński per n=1,2,... , costituiscono una successione di curve piane chiuse continue definite per ricorrenza scoperte da Wacław Sierpiński, che nel limite riempiono completamente la superficie del quadrato unitario: per questo la loro curva limite, anche nota come la curva di Sierpiński, è un esempio di una curva che riempie lo spazio.
Dato che la curva di Sierpiński ricopre il piano, la sua dimensione di Hausdorff (nel limite ) è .
La lunghezza euclidea di è , cioè cresce esponenzialmente con oltre ogni limite, mentre il limite per dell'area inclusa da è di quella del quadrato (nella metrica euclidea).
-
Curva di Sierpiński al primo ordine
-
Curva di Sierpiński
di ordine da 1 a 2 -
Curva di Sierpiński
di ordine da 1 a 3
Utilizzi della curva
[modifica | modifica wikitesto]La curva di Sierpiński è utile in diverse applicazioni pratiche, perché è la più simmetrica tra le curve che ricoprono il piano più comunemente studiate. Per esempio, è stata usata come base per la costruzione rapida di una soluzione approssimata del problema del commesso viaggiatore ( che chiede il percorso più breve che tocca tutti gli elementi di un insieme assegnato di punti): il procedimento euristico consiste nel visitare i punti nella stessa sequenza come appaiono nella curva di Sierpiński [1]. Per fare ciò è necessario eseguire due passaggi: primo calcolare un'immagine inversa per ogni punto che deve essere visitato; poi riordinare i valori. Questa idea è stata utilizzata per costruire i sistemi di percorso per i veicoli commerciali, basati sui file Rolodex [2].
Una curva che ricopre il piano è una mappa continua dell'intervallo unitario sul quadrato unitario e quindi un'applicazione (pseudo) inversa mappa il quadrato unitario sull'intervallo unitario. Un modo per costruire una pseudo inversa è il seguente. Si faccia corrispondere l'angolo in basso a sinistra (0,0) del quadrato unitario al punto 0.0 (e 1.0). Quindi l'angolo in alto a sinistra (0,1) deve corrispondere a 0.25, l'angolo in alto a destra (1,1) a 0.50 e l'angolo in basso a destra (1,0) a 0.75. La funzione inversa dei punti interni si calcola utilizzando la struttura ricorsiva della curva. Qui di seguito si trova una funzione codificata in linguaggio Java che calcola le posizioni relative di ogni punto sulla curva di Sierpiński (cioè un valore pseudo-inverso). Essa utilizza come input le coordinate del punto (x,y) da convertire e le coordinate dei vertici di un triangolo isoscele che lo include (ax, ay), (bx, by), e (cx, cy) (Notare che il quadrato unitario è l'unione di due triangoli di questo tipo). I parametri rimanenti specificano il livello di accuratezza al quale si deve calcolare l'inverso.
static long sierp_pt2code( double ax, double ay, double bx, double by, double cx, double cy,
int currentLevel, int maxLevels, long code, double x, double y )
{
if (currentLevel <= maxLevel) {
currentLevel ++;
if ((sqr(x-ax) + sqr(y-ay)) < (sqr(x-cx) + sqr(y-cy))) {
code = sierp_pt2code( ax, ay, (ax+cx)/2.0, (ay+cy)/2.0, bx, by,
currentLevel, maxLevel, 2 * code + 0, x, y );
}
else {
code = sierp_pt2code( bx, by, (ax+cx)/2.0, (ay+cy)/2.0, cx, cy,
currentLevel, maxLevel, 2 * code + 1, x, y );
}
}
return code;
}
Disegnare la curva
[modifica | modifica wikitesto]Il seguente applet Java disegna una curva di Sierpiński con quattro metodi che si richiamano l'un l'altro ricorsivamente:
import java.awt.*; import java.applet.*;
public class SierpinskiCurve extends Applet {
private SimpleGraphics sg=null;
private int dist0 = 128, dist;
public void init() {
sg = new SimpleGraphics(getGraphics());
dist0 = 128;
resize ( 4*dist0, 4*dist0 );
}
public void paint(Graphics g) {
int level = 3;
dist = dist0;
for (int i=level;i>0;i--) dist /= 2;
sg.goToXY(2*dist,dist);
sierpA(level); // start recursion
sg.lineRel(+dist,+dist);
sierpB(level); // start recursion
sg.lineRel(-dist,+dist);
sierpC(level); // start recursion
sg.lineRel(-dist,-dist);
sierpD(level); // start recursion
sg.lineRel(+dist,-dist);
}
private void sierpA (int level) {
if (level > 0) {
sierpA(level-1); sg.lineRel(+dist,+dist);
sierpB(level-1); sg.lineRel(+2*dist,0);
sierpD(level-1); sg.lineRel(+dist,-dist);
sierpA(level-1);
}
}
private void sierpB (int level) {
if (level > 0) {
sierpB(level-1); sg.lineRel(-dist,+dist);
sierpC(level-1); sg.lineRel(0,+2*dist);
sierpA(level-1); sg.lineRel(+dist,+dist);
sierpB(level-1);
}
}
private void sierpC (int level) {
if (level > 0) {
sierpC(level-1); sg.lineRel(-dist,-dist);
sierpD(level-1); sg.lineRel(-2*dist,0);
sierpB(level-1); sg.lineRel(-dist,+dist);
sierpC(level-1);
}
}
private void sierpD (int level) {
if (level > 0) {
sierpD(level-1); sg.lineRel(+dist,-dist);
sierpA(level-1); sg.lineRel(0,-2*dist);
sierpC(level-1); sg.lineRel(-dist,-dist);
sierpD(level-1);
}
}
}
class SimpleGraphics {
private Graphics g = null;
private int x = 0, y = 0;
public SimpleGraphics(Graphics g) { this.g = g; }
public void goToXY(int x, int y) { this.x = x; this.y = y; }
public void lineRel(int deltaX, int deltaY) {
g.drawLine ( x, y, x+deltaX, y+deltaY );
x += deltaX; y += deltaY;
}
}
Note
[modifica | modifica wikitesto]- ^ Platzman, Loren K. and John J. Bartholdi, III (1989). "Spacefilling curves and the planar traveling salesman problem", Journal of the Association of Computing Machinery 36(4):719-737.
- ^ Bartholdi, John J. III, Some combinatorial applications of spacefilling curves Archiviato il 3 agosto 2012 in Archive.is.
Voci correlate
[modifica | modifica wikitesto]- Curva di Sierpiński in Triangolo di Sierpiński
- Curva di Hilbert
- Curva di Peano
- Fiocco di neve di Koch
- Lista di frattali per dimensione di Hausdorff
Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file sulla Curva di Sierpiński
Wikimedia Commons contiene immagini o altri file sulla Curva di Sierpiński
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Sierpiński curve, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Curva di Sierpiński, su MathWorld, Wolfram Research.
- Giorgio Pietrocola, Curva di Peano-Sierpinski (animazione didattica), su Maecla,Tartapelago, 2007. URL consultato il 27 dicembre 2018.