Simmetria (fisica)

In fisica il concetto di simmetria identifica la proprietà dei fenomeni fisici di ripetersi sostanzialmente identici nel tempo e nello spazio.

Fino alla fine dell'Ottocento, pur essendo chiaro che in fisica dovevano venire rispettate certe invarianze, non se ne parlava esplicitamente in quanto ciò appariva banale. Con l'introduzione della teoria della relatività ristretta, le invarianze hanno assunto grande importanza, in quanto caratteristiche essenziali dei fenomeni fisici. È infatti fondamentale che le leggi fisiche che li descrivono non dipendano dalla loro posizione spazio-temporale rispetto all'osservatore, ma che siano invarianti rispetto ad esso. Se così non fosse, ogni osservatore vedrebbe i fenomeni in maniera inconciliabile con altri osservatori e le sue stesse osservazioni varierebbero da istante a istante e da luogo a luogo.

In altri termini, le leggi che descrivono le regolarità della natura devono essere invarianti per spostamenti nel tempo e nello spazio. Per questo ci si appoggia all'idea di simmetria, un concetto di facile visualizzazione nel campo della geometria, ma che si può applicare anche ad enti non geometrici, come appunto le leggi empiriche. Nel linguaggio comune non vi è una relazione molto stretta fra i concetti di invarianza e di simmetria, mentre in fisica invarianza e simmetria sono sinonimi. Vi sono diversi tipi di simmetria e tutti si possono descrivere mediante la teoria dei gruppi.

In prima approssimazione, una figura geometrica si dice simmetrica se rimane uguale a sé stessa in seguito a qualche trasformazione. Per esempio, un quadrato rimane invariato in seguito a rotazioni di 90° intorno a un asse che passa per il suo centro ortogonalmente al piano su cui è definito. Questo significa che per rotazioni qualsiasi ogni punto del quadrato è mappato in un punto diverso ma che per certe rotazioni l'intero quadrato è mappato su sé stesso.

Una simmetria geometrica è un'invarianza rispetto a una trasformazione subita da una figura geometrica.

Il concetto di uguaglianza è centrale in simmetria ma, per estendere l'idea di simmetria oltre l'ambito della geometria, occorre introdurre l'idea di uguaglianza relativa: due oggetti sono detti uguali rispetto a qualche caratteristica se entrambi possiedono tale caratteristica. Non fa differenza se si tratta di due oggetti distinti o del medesimo oggetto che ha subito qualche trasformazione. L'oggetto può essere una figura geometrica, un oggetto fisico, un concetto astratto qualsiasi: in generale un sistema. Quello di sistema è il concetto più generale che si possa adottare. Può essere una figura geometrica (mono, bi o tri-dimensionale), un oggetto (una molecola, un cristallo, un essere vivente o una sua parte), un processo dinamico, ovvero variabile nel tempo (il moto di un oggetto, l'accrescimento di un organismo, una reazione chimica, lo sviluppo del calcolo in un computer), o addirittura un concetto astratto (oggetti matematici come funzioni o matrici, leggi empiriche, ecc.).

Se ${\displaystyle T}$, ad esempio, è una trasformazione che porta un sistema da uno stato iniziale a una sua immagine, tale trasformazione può venire combinata con un'altra in un modo che ricorda la somma fra numeri: due trasformazioni ${\displaystyle T}$ successive equivalgono a un'unica rotazione di 180°. Questo rimane vero per due trasformazioni qualsiasi.

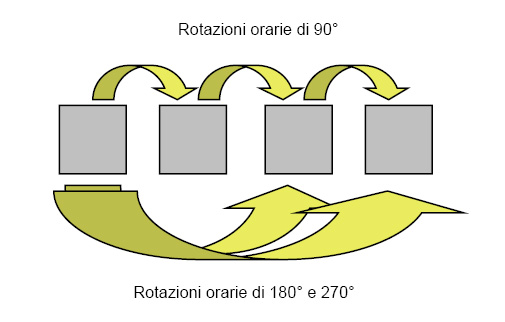
Si definisce anche una trasformazione inversa, che riporta il sistema nello stato iniziale. Il numero di tali trasformazioni è un indice del grado di simmetria del sistema. Per esempio, un quadrato è più simmetrico di un triangolo equilatero perché ha quattro possibili rotazioni intorno al centro che portano alla sovrapposizione (0°, 90°, 180° e 270°), invece di tre solamente (0°, 120°, 240°) ed è meno simmetrico di un esagono, che ha sei rotazioni possibili (60° e multipli di questa).

Le simmetrie geometriche più note sono associate a rotazioni intorno a un asse, come nel caso del quadrato, che ruota sul piano, intorno a un asse verticale passante per il centro. Con maggiore precisione va detto che nel caso di rotazioni superiori a ${\displaystyle 2\pi }$, tutti i punti dell'oggetto tornano a occupare la medesima posizione occupata dopo una delle rotazioni in figura, il che rende assolutamente indistinguibile l'oggetto prima e dopo ulteriori rotazioni di ${\displaystyle 2n\pi }$, in verso orario o antiorario.

Le simmetrie geometriche si riferiscono alla posizione della figura di cui si tratta. Più in generale si parla di stato di un sistema. Per esempio, il prodotto ${\displaystyle pV}$, fra pressione ${\displaystyle p}$ e volume ${\displaystyle V}$ di un gas ideale è invariante rispetto a variazioni di ${\displaystyle V}$ a temperatura costante.

Un cerchio, poi, è la figura piana più simmetrica, poiché è simmetrico per infinite rotazioni intorno all'asse che passa per il suo centro. Si tratta di una delle molte situazioni limite che, vedremo, hanno un interesse particolare.

Lo stesso argomento in dettaglio: Gruppo (matematica).

È possibile effettuare una trattazione formale delle simmetrie facendo ricorso alla teoria dei gruppi. Un gruppo è un insieme ${\displaystyle G}$ di elementi (o trasformazioni) più un'operazione di composizione fra due di loro, ${\displaystyle a}$ e ${\displaystyle b}$, che denotiamo ${\displaystyle ab}$ tale che:

1. il risultato dell'operazione sia anch'essa un elemento dell'insieme (${\displaystyle G}$ è chiuso)
2. l'operazione sia associativa ${\displaystyle a(bc)=(ab)c}$
3. vi sia un elemento speciale di ${\displaystyle G}$, detto identità ${\displaystyle I}$, tale che per ogni elemento ${\displaystyle a}$ dell'insieme sia ${\displaystyle aI=Ia=a}$
4. per ogni elemento ${\displaystyle a}$ vi sia un elemento ${\displaystyle a'}$, appartenente all'insieme, che si dice inverso di ${\displaystyle a}$, tale che ${\displaystyle aa'=a'a=I}$

Se poi vale anche la proprietà commutativa ${\displaystyle ab=ba}$, il gruppo si dice commutativo, o abeliano, altrimenti è non commutativo.

Il numero degli elementi che appartengono a ${\displaystyle G}$ è detto ordine del gruppo.

L'insieme dei numeri interi relativi con l'operazione di somma è un gruppo commutativo infinito se l'identità ${\displaystyle I}$ è lo zero e l'inverso è il contrario di ${\displaystyle a:a'=-a}$. Se invece consideriamo l'insieme dei numeri interi relativi con l'operazione di moltiplicazione, ${\displaystyle I=1}$, dove l'inverso assume il significato usuale ${\displaystyle a'=1/a}$, quindi non è un intero e per lo zero non è neppure definito, non siamo in presenza di un gruppo. È un altro tipo di struttura algebrica, denominata monoide, che presenta solo la proprietà associativa e l'esistenza dell'elemento neutro, detto anche semigruppo con neutro.

Nel caso di un quadrato, per ogni rotazione esiste una rotazione inversa e vi è una proprietà commutativa. È poi facile dimostrare che è valida la proprietà associativa. L'elemento ${\displaystyle I}$ non coincide con alcuna trasformazione o, che è lo stesso, coincide con una rotazione di 360°. L'operazione di associazione è l'esecuzione in successione di due trasformazioni.

Le rotazioni orarie di un quadrato e l'associazione di due qualsiasi di esse costituiscono quindi un gruppo di ordine 4. Le rotazioni intorno all'asse che passa per il centro non sono le sole trasformazioni di simmetria possibili con un quadrato. Vi sono anche riflessioni speculari lungo gli assi e le diagonali, che costituiscono un altro gruppo.

L'insieme di tutte le trasformazioni di simmetria di un dato sistema costituisce il suo gruppo di simmetria, includendo come elemento identità la trasformazione nulla, ovvero "non fare alcuna operazione", nella quale ogni elemento del sistema è mappato su sé stesso. Il gruppo di simmetria del quadrato risulta quindi dall'unione dei sottogruppi delle rotazioni e delle riflessioni, che già comprendono l'identità.

Vi può essere un solo gruppo astratto di ordine ${\displaystyle 1}$ ed è costituito dal solo elemento identità. Si realizza, per esempio, nel gruppo costituito dallo zero e dalla somma come operazione di composizione. Lo zero, come si è visto, è infatti l'identità del gruppo dei numeri interi e somma. Vi è pure un solo gruppo astratto di ordine ${\displaystyle 2}$, costituito dall'identità e da un elemento ${\displaystyle a}$, quindi si pone la necessità di includere pure l'inverso di ${\displaystyle a}$: questo deve coincidere col suo inverso e quindi ${\displaystyle a\,a=I}$. Una realizzazione numerica di tale gruppo è costituita dai numeri ${\displaystyle 1}$ (identità) e ${\displaystyle -1}$ sotto l'operazione di moltiplicazione.

Altre realizzazioni del medesimo gruppo sono, in geometria:

1. il gruppo costituito dall'identità (nessuna trasformazione) e dalla riflessione, con operazione di composizione costituita da due riflessioni consecutive 4
2. la rotazione di un oggetto di 0° (identità) e di 180° intorno a un asse, con composizione costituita da due rotazioni successive di 180°.

Questi gruppi si realizzano facilmente usando rispettivamente due specchietti e un quaderno a spirale. Entrambi si realizzano poi nella simmetria bilaterale, tipica degli animali.

I gruppi di simmetria che realizzano il medesimo gruppo astratto si dicono isomorfi, in quanto le loro tabelle di moltiplicazione hanno la medesima struttura. Si tratta di una proprietà molto importante, con risvolti interessanti in fisica, in quanto sistemi isomorfi presentano interessanti identità di comportamento che si riflettono nelle descrizioni dei fenomeni associati ai sistemi stessi.

Anche per un gruppo di ordine 3 vi è un solo gruppo astratto. Siccome il gruppo deve contenere l'inverso delle trasformazioni e qui vi sono solo due elementi, ${\displaystyle b}$ deve essere l'inverso di ${\displaystyle a}$ e, naturalmente, viceversa.

Fra le realizzazioni di questo gruppo consideriamo un triangolo equilatero e le sue rotazioni intorno a un asse che passa per il centro del triangolo. L'identità è nessuna rotazione, ${\displaystyle a}$ è una rotazione di 120° e ${\displaystyle b}$ una rotazione di 240°, entrambe in senso orario.

Ogni sequenza rettilinea periodica gode di simmetria per traslazione, purché sia infinita, altrimenti, dopo una traslazione più o meno ampia, la sequenza finisce e la simmetria si rompe. In questo caso si ha una simmetria approssimata, valida entro un ambito più o meno ampio.

In particolare, gode di simmetria di traslazione una retta. Questa è un caso limite di traslazione, perché continua. Il simbolo è ${\displaystyle (a_{0})}$. La traslazione può avvenire nello spazio e anche nel tempo, basta pensare che questo può venire rappresentato dalla scansione dei giorni, delle ore, dei secondi, ... lungo una retta (che però dovrebbe essere infinita).

Nel corso della traslazione i punti della retta lungo la quale scivola la struttura che si sposta rimangono al loro posto: tale retta si dice asse di traslazione. La ragione di tale definizione si chiarisce meglio se la struttura che trasla è una banda, naturalmente infinita. L'asse di traslazione, in quanto rimane invariato nel corso della traslazione, si dice un elemento singolare della simmetria. Dato che tutte le rette parallele hanno la medesima direzione, l'asse di traslazione si indica con una qualsiasi retta parallela alla retta o all'asse della banda che traslano.

In biologia esempi di simmetria approssimata per spostamento nel tempo sono i vari ritmi circadiani, che si osservano nella biochimica e nel comportamento di tutti gli animali e vegetali. In chimica lo sono le svariate reazioni oscillanti. In fisica lo sono tutti i moti periodici, in particolare i moti dei pianeti nel sistema solare. La cosmologia moderna prevede che il tempo abbia avuto un inizio, in corrispondenza del big bang, ovvero della prima formazione dell'universo. Quindi la simmetria per traslazione del tempo è accettabilissima oggi, anche per fenomeni di durata molto lunga, ma va vista con molta cautela in astrofisica.

Le traslazioni lungo un asse ${\displaystyle a}$ (senza specificarne il verso), con l'operazione di composizione realizzata da due traslazioni successive, costituiscono un gruppo, che si indica con il simbolo ${\displaystyle a}$^{[Con lo stesso simbolo si indicano l'asse, il gruppo e un elemento del gruppo?]}. Infatti si vede immediatamente che sono soddisfatte le condizioni:

• il risultato di due traslazioni successive è anch'esso una traslazione
• le traslazioni si possono associare a piacere: per tre traslazioni successive ${\displaystyle a,\,b}$ e ${\displaystyle c}$ si ha ${\displaystyle (ab)c=a(bc)}$
• l'identità equivale a nessuna traslazione (spostamento nullo)
• per ogni traslazione ${\displaystyle a}$ in un verso dell'asse di traslazione ne esiste una contraria nel verso opposto, ${\displaystyle a'}$, che riporta il sistema nello stato di partenza.

Il gruppo limite delle traslazioni continue, con passo infinitesimo, si denota ${\displaystyle a0}$. Il gruppo, di ordine infinito, delle traslazioni in una dimensione è un sottogruppo dei gruppi delle traslazioni negli spazi pluridimensionale. Una retta è omogenea, nel senso che le sue proprietà non cambiano da segmento a segmento. Una retta rappresenta l'asse, continuo, dei numeri reali. Una traslazione lascia invariate le distanze fra coppie di punti, cioè le differenze fra i numeri che essi rappresentano. È quindi indifferente la posizione dell'origine dell'asse.

La simmetria per riflessione è quella che banalmente si osserva tutti i giorni guardandosi allo specchio.

In una dimensione questa si riferisce a oggetti con andamento lineare, come i fregi decorativi o una macromolecola lineare e si verifica ogni volta che una struttura si ripete identica per riflessione rispetto a un centro di riflessione.

Il punto in corrispondenza del quale si immagina di disporre lo specchio è il solo punto del sistema che non si mappa in punto diverso nel corso della trasformazione. È quindi un punto singolare che viene detto centro di riflessione. Il piano di riflessione viene detto ${\displaystyle \mathbf {m} }$ (da mirror) e il gruppo delle simmetrie per riflessione si denota ${\displaystyle \mathbf {m'} }$.

Di solito, muovendosi in un verso prefissato lungo l'oggetto e la sua immagine, si incontrano le diverse parti dell'oggetto e dell'immagine in un ordine diverso.

Simmetrie per spostamento e per riflessione si osservano anche fra suoni lungo l'asse del tempo. Per esempio, il battito regolare di uno strumento che scandisce il ritmo di un rap è traslabile nel tempo esattamente come per una struttura ripetitiva lungo un asse nello spazio geometrico.

Se, invece, avessimo a che fare con una figura più omogenea, per esempio di tutti triangoli, lo spazio sarebbe isotropo, almeno su una scala macroscopica, tale da consentire di trascurare la disomogeneità dovuta all'accostamento dei triangoli. Solo con una figura continua, come una retta o una barra avremmo contemporaneamente omogeneità ed isotropia.

Combinazioni di traslazioni e riflessioni si ritrovano in strutture musicali ben più complesse di una scala, come la fuga, e nella struttura ritmica della poesia. Una riflessione particolarmente importante in fisica riguarda il tempo. Malgrado questo scorra irreversibilmente, è possibile porre in un istante qualsiasi l'origine dei tempi, come appena osservato per l'asse dei numeri reali e considerare i tempi negativi come tempi storici.

L'operazione di inversione del tempo viene detta anche trasformazione ${\displaystyle t\to -t}$. Le leggi della fisica sono spesso invarianti rispetto a tale trasformazione. Far scorrere il tempo all'indietro è come riavvolgere un film. È l'invarianza delle leggi rispetto a traslazione e inversione del tempo che consente ai cosmologi di discutere sull'origine dell'universo, utilizzando conoscenze e osservazioni odierne, nonché di interpretare in base a teorie vecchie di pochi decenni osservazioni astronomiche odierne di fenomeni che, in conseguenza della velocità finita della luce, sono avvenuti miliardi di anni fa.

Se consideriamo l'uguaglianza relativa alla forma e alle dimensioni di un oggetto (per ora piano) è evidente che questo rimane uguale a sé stesso in qualsiasi posizione si trovi rispetto a chi guarda. Possiamo anche pensare di lasciare l'oggetto dove sta, mentre chi osserva si sposta. Quindi si può avere simmetria di traslazione anche sul piano, nello spazio tridimensionale e in spazi di ordine superiore.

Sul piano si identificano due direzioni di traslazione principali. Le traslazioni in tutte le altre direzioni si ottengono per composizione di traslazioni lungo i due assi principali. Uno di questi viene chiamato ${\displaystyle \mathbf {a} }$, l'altro viene detto ${\displaystyle \mathbf {b} }$. L'insieme di tutte le traslazioni possibili costituiscono il gruppo delle traslazioni piane, denotato come ${\displaystyle \mathbf {a} :\mathbf {b} }$ se i due assi sono perpendicolari fra di loro, ${\displaystyle \mathbf {a} /\mathbf {b} }$ se sono obliqui.

È evidente che il gruppo delle traslazioni lungo una retta, che abbiamo chiamato ${\displaystyle a}$, è un sottogruppo del gruppo delle traslazioni piane ${\displaystyle ab}$, che a sua volta comprende ${\displaystyle a:b}$ e ${\displaystyle a/b}$. Vedremo poi che tutti quelli citati sono sottogruppi del gruppo delle traslazioni in uno spazio a tre dimensioni, che, a sua volta, si può estendere a spazi di qualsiasi dimensione.

La simmetria per riflessione si ha quando un sistema si trasforma come riflesso da uno specchio perpendicolare al piano. Come in una dimensione, la riflessione, con composizione data da due riflessioni successive ha due soli stati, iniziale e riflesso, e l'identità è il ricoprimento dello stato iniziale. Costituisce il gruppo ${\displaystyle m}$ di ordine 2 delle riflessioni in ${\displaystyle 1,\,\ldots ,\,n}$ dimensioni.

In alcune figure si ha simmetria di riflessione quando ogni punto della figura è riflesso rispetto a un centro di riflessione intersezione di due o più assi di riflessione. In figure con numero pari di lati, e altre, come la stella di Davide o la parabola cubica, la riflessione viene a coincidere con una rotazione di 180º. Centri, assi e piani di riflessione sono elementi singolari, in quanto non subiscono spostamenti di sorta in seguito alla trasformazione di simmetria.

Si ha simmetria di rotazione quando un sistema rimane invariante per rotazioni intorno a un asse perpendicolare al piano, ovvero intorno al centro della figura, come nel caso del triangolo equilatero, del quadrato, della stella e dell'esagono.

La croce allungata, pur avendo due piani di simmetria speculare, ha solo due posizioni di ricopertura per rotazioni intorno all'asse che passa per il centro (180° e 360°) e quindi tale asse viene indicato con 2. Viene detto asse binario (two-fold). Come già osservato, nel caso del quadrato si ha simmetria per rotazioni di 90º, 180º e 270º ma si ha riflessione speculare anche rispetto agli assi che passano per i vertici e i centri dei lati opposti. Anche nel caso dell'esagono, oltre a 6 rotazioni, si ha simmetria per riflessione pure lungo gli assi che passano per i vertici e i centri dei lati opposti. Il cerchio è simmetrico per infinite rotazioni intorno al centro.

Mentre l'insieme delle trasformazioni di simmetria, dell'identità e dell'operazione di trasformazione costituisce il gruppo di simmetria del sistema considerato, l'insieme degli elementi della simmetria (assi, piani, centri) costituisce la classe di simmetria del sistema. Il quadrato e la croce hanno la medesima classe di simmetria, e così pure l'esagono e la stella a cinque punte hanno rispettivamente la medesima classe della stella di Davide e del pentagono.

Le rotazioni intorno a un asse di una data figura, con identità costituita da nessuna rotazione e operazione di composizione data da due rotazioni successive costituiscono un gruppo di ordine pari al numero di ricoperture della figura che si hanno in una rotazione di 360º. L'asse di rotazione si indica semplicemente con il numero delle posizioni di ricopertura: 4 per un quadrato, 6 per un esagono, fino a infinite per un cerchio.

Nella notazione della classe, la coesistenza dei gruppi di rotazione e di riflessione viene denotata con un punto ⋅ se l'asse di rotazione e il piano di riflessione sono paralleli, con due punti : se sono perpendicolari fra di loro.

Lo stesso argomento in dettaglio: Chiralità (fisica).

Alcune emifigure si possono portare a coincidere per rotazione sul piano, intorno a un asse perpendicolare al piano stesso (tutte quelle con asse di rotazione di ordine pari, ma questa non va presa per una regola assoluta) altre vengono a coincidere solo e soltanto per riflessione.

Si dicono chirali, o enantiomorfi, i sistemi che possono venire portati a coincidere solo per riflessione e non tramite qualsiasi altra trasformazione di simmetria.

Sistemi chirali sono comuni in natura e la chiralità, o la sua assenza, impartisce al sistema proprietà importanti. Nel mondo biologico ha una particolare importanza la simmetria bilaterale, caratterizzata da un unico piano di riflessione, ma sono frequentissime simmetrie con chiralità di ordine più elevato, come nelle stelle di mare. Il concetto di chiralità si collega alla definizione di destra e sinistra, ovvero a quella di rotazione oraria o antioraria. Nella fisica macroscopica tali definizioni sono del tutto arbitrarie e convenzionali. Non esiste fenomeno macroscopico che implichi una speciale definizione di destra e sinistra, e quindi di orario e antiorario: le leggi che descrivono i fenomeni non cambiano se ci poniamo di fronte al sistema che si osserva, con una scelta ben definita di destra e sinistra, ovvero se ci poniamo dietro il sistema, o lo ruotiamo di 180°, invertendo in tal modo destra e sinistra. I fenomeni macroscopici sono invarianti rispetto allo scambio destra-sinistra, ovvero rispetto alla riflessione.

In geometria si dicono congruenti due sistemi ${\displaystyle S}$ ed ${\displaystyle S'}$ quando ogni punto di ${\displaystyle S}$ si mappa in un punto di ${\displaystyle S'}$ mantenendo invariata la distanza fra due punti ${\displaystyle A}$ e ${\displaystyle B}$ di ${\displaystyle S}$ e i corrispondenti punti ${\displaystyle A'}$ e ${\displaystyle B'}$ di ${\displaystyle S'}$. La congruenza è quindi un tipo particolare di mappa nella quale si conservano le distanze e gli angoli.

Questo, appunto, avviene fra una figura geometrica e la sua immagine ottenuta per traslazione, rotazione e riflessione speculare, ma il discorso si può estendere a un sistema qualsiasi, definendo in maniera opportuna la distanza fra i suoi punti. Ciò si verifica immediatamente in sistemi rappresentabili in uno spazio euclideo, dato che in questo caso si definisce facilmente la distanza tra due punti.

Dati tre punti non allineati ${\displaystyle A,\,B,}$ e ${\displaystyle C}$ nel sistema considerato (per esempio i vertici di un triangolo) e i corrispondenti ${\displaystyle A',\,B',}$ e ${\displaystyle C'}$ nella sua immagine, nella traslazione e rotazione si percorre la successione ${\displaystyle A'\,B'\,C'}$ nello stesso ordine (in verso orario o antiorario) nel quale si percorre la terna corrispondente ${\displaystyle A\,B\,C}$. La congruenza si dice diretta. Nella riflessione, invece, la terna ${\displaystyle A'\,B'\,C'}$ si percorre in senso antiorario se ${\displaystyle A\,B\,C}$ sono disposti in senso orario, e viceversa. La congruenza si dice allora inversa. In questo caso il sistema e la sua immagine congruente sono chirali. Le congruenze non comprendono peraltro tutte le possibili invarianze. Una simmetria importante in fisica e in geometria è collegata alla trasformazione di dilatazione. In essa i punti di una figura allineati con un punto, detto centro di dilatazione, vengono mappati in punti più vicini o più lontani di un dato fattore di dilatazione. Per dilatazione si costruiscono, per esempio, triangoli simili, invarianti rispetto alla forma ma non rispetto alle dimensioni. Nella relatività interessano le dilatazioni del tempo e della lunghezza dei regoli.

Le simmetrie di rotazione e di riflessione sono collegate fra di loro, e quindi alla chiralità. Le figure con simmetria di rotazione di ordine dispari possiedono sempre parti chirali, ma non è detto che le simmetrie di rotazione di ordine pari comportino sempre la presenza di emisistemi non chirali. Il che conferma che le riflessione non è un caso particolare della rotazione.

Si tratta di un gruppo tridimensionale, in quanto viene generato da tre diverse simmetrie, ognuna col proprio elemento di simmetria. Queste sono:

1. traslazioni nella direzione dell'asse x, elemento di simmetria ${\displaystyle a0}$
2. traslazioni nella direzione dell'asse y, elemento di simmetria ${\displaystyle b0}$
3. rotazioni sul piano ${\displaystyle (x,y)}$, elemento di simmetria: ${\displaystyle \infty }$

La classe di simmetria di tale spazio è quindi ${\displaystyle a0:b0}$ : ${\displaystyle \infty }$.

In tre dimensioni non si introducono nuovi elementi di simmetria, oltre a quelli già visti, ma è importante l'aumento delle loro possibilità di composizione, che consente di descrivere situazioni molto rilevanti dal punto di vista fisico.

Vi sono due gruppi di oggetti tridimensionali particolarmente importanti: i reticoli e i solidi geometrici. I primi portano, in particolare, alla descrizione dei reticoli cristallini e alla stereochimica. Le classi di simmetria dei solidi sono invece importanti per la descrizione di svariati fenomeni fisici, fra i quali i campi gravitazionale, elettrico e magnetico.

I reticoli spaziali sono sistemi discontinui, estensione di analoghi sistemi mono e bi-dimensionali. In essi, quindi, esistono tre assi di traslazione, perpendicolari fra di loro ${\displaystyle a:b:c}$, oppure inclinati, ${\displaystyle a:b/c}$, ${\displaystyle a/b/c}$ ecc., e, come sempre, la simmetria di traslazione è perfetta solo per reticoli infiniti e si rompe in prossimità dei margini dei reticoli finiti, dove, quindi, possiamo aspettarci bruschi cambiamenti nelle proprietà fisiche.

Anche nella situazione tridimensionale vi è una classe limite di traslazioni continue, con passo infinitamente piccolo ${\displaystyle (a0:b0:c0)}$, il quale assicura che lo spazio è omogeneo, non solo nella direzione degli assi principali ma anche in tutte le direzioni definite da spostamenti qualsivoglia lungo di questi. Lo spazio è quindi omogeneo, come già osservato a proposito di una retta, e anche isotropo, in quanto le sue proprietà non cambiano con la direzione. Alle traslazioni continue si sovrappongono poi gruppi di rotazione e riflessione che influiscono sull'isotropia dello spazio. I continui tridimensionali sono importanti per descrivere le proprietà dei campi, gravitazionale, elettrico, ecc. e anche situazioni macroscopiche nelle quali lo spazio è approssimativamente continuo, ovvero quando sono in gioco dimensioni spaziali molto più grandi di quelle di una cella del reticolo stesso. In tal caso omogeneità e isotropia sono approssimate. Le riflessioni sono realizzazioni del medesimo gruppo ${\displaystyle m}$.

Le barre sono il corrispondente tridimensionale delle bande piane. Queste sono dei nastri a una o due facce, di lunghezza infinita e caratterizzati da due elementi singolari, l'asse di traslazione e un piano (che contiene l'asse) sul quale scivola la banda quando trasla. Le barre, invece, sono oggetti tridimensionali di varia sezione, ma sempre di lunghezza infinita, caratterizzati da un solo elemento singolare: l'asse di traslazione.

Consideriamo una barra a sezione triangolare equilatera. Questa ha un asse di traslazione singolare, che facciamo arbitrariamente passare per il centro del triangolo ed è un elemento limite ${\displaystyle (a0)}$, in quanto consente spostamenti infinitesimi. Questo asse coincide con un asse di rotazione ternario sul quale si intersecano tre piani di riflessione ${\displaystyle m\cdot 3}$, Vi sono poi infiniti piani di riflessione come quello in azzurro nella figura, uno per ognuna delle infinite traslazioni possibili e perpendicolari ai tre che corrispondono alle rotazioni. La classe di simmetria risulta quindi ${\displaystyle (a0)m\cdot 3:m}$.

In un prisma triangolare scompare l'asse di traslazione continuo e quindi degli infiniti piani di riflessione perpendicolari all'asse di rotazione rimane solo quello in corrispondenza della mezzeria. La classe di simmetria si riduce allora a ${\displaystyle m\cdot 3:m}$. Una barra e un prisma a sezione quadrata hanno un asse di rotazione quaternario anziché ternario. Le rispettive classi sono quindi ${\displaystyle (a0)\cdot m\cdot 3:m}$ e ${\displaystyle m\cdot 4:m}$. Queste si riducono a ${\displaystyle (a0)\cdot m\cdot 2:m}$ e ${\displaystyle m\cdot 2:m}$ rispettivamente per barre e prismi a sezione rettangolare, con un asse di rotazione binario e due piani di riflessione longitudinali. In generale, pertanto, la classe di simmetria delle barre prismatiche è ${\displaystyle (a0)\cdot m\cdot n:m}$ e quella dei rispettivi prismi finiti ${\displaystyle m\cdot n:m}$, dove ${\displaystyle n}$ è il numero delle rotazioni di 360°/n che portano alla ricopertura nel corso di una rotazione complessiva di 360°. Per una barra a sezione circolare, dove n è infinito, la classe di simmetria diviene la classe limite ${\displaystyle (a0)\cdot m\infty :m}$.

Notare che il centro della sezione di intersezione dei piani di riflessione trasversali con il cilindro è un centro di simmetria per la barra cilindrica e per quelle con sezioni regolari con un numero pari di piani di riflessione. Infatti a ogni punto ${\displaystyle P}$ della barra da una parte del centro ne corrisponde uno ${\displaystyle P'}$ a uguale distanza dall'altra parte. Va pure considerato che, fino a questo momento le barre e i solidi finiti sono stati considerati fermi. L'introduzione di un movimento di traslazione o di rotazione ne modifica la simmetria. L'asse di traslazione diviene infatti polare, in quanto il percorrerlo nell'uno o nell'altro verso vuol dire andare nel verso del moto oppure nel verso opposto. E pure le rotazioni del cilindro possono essere nel verso del suo moto rotatorio o in quello opposto.

Nel primo caso vengono a mancare i piani di riflessioni trasversali, in quanto essi rifletterebbero il moto longitudinale nel verso sbagliato. Le classi di simmetria delle barre e dei solidi di lunghezza finita si riducono quindi a ${\displaystyle (a0)\cdot n\cdot m}$ e ${\displaystyle n\cdot m}$. Nel secondo caso si perdono invece, per motivi analoghi, i piani di riflessione longitudinali e le classi di simmetria diventano ${\displaystyle (a0)\cdot n:m}$ e ${\displaystyle n:m}$.

Lo stesso argomento in dettaglio: Teorema di Noether.

Il teorema di Noether sancisce un legame tra l'invarianza di una certa quantità rispetto a trasformazioni di uno o più campi e la legge di conservazione di una corrente, detta appunto corrente di Noether. Fu dimostrato dalla matematica Emmy Noether nel 1915 e pubblicato nel 1918.^[1]

Il teorema di Noether vale solo per leggi di conservazione locali, altrimenti non vi sarebbe una corrente associata. Ad oggi, tutte le leggi di conservazione conosciute sono locali.

Il teorema di Noether afferma con precisione che

A ogni simmetria differenziabile generata da azioni locali corrisponde una corrente conservata.

Se un sistema lagrangiano ammette un gruppo di trasformazioni delle coordinate ad un parametro ${\displaystyle s}$

${\displaystyle \mathbf {q} =\mathbf {F} (\mathbf {Q} ,s)}$

tale che la lagrangiana sia invariante rispetto a tale trasformazione

${\displaystyle {\mathcal {L}}(\mathbf {q} ,\mathbf {\dot {q}} )={\mathcal {L}}(\mathbf {Q} ,\mathbf {\dot {Q}} )}$

allora il gruppo è di simmetria e il sistema ha un integrale primo dato da

${\displaystyle {\mathcal {I}}(\mathbf {Q} ,\mathbf {\dot {Q}} )=\sum _{i}{\frac {\partial {\mathcal {L}}}{\partial \mathbf {\dot {q}} _{i}}}(\mathbf {q} ,\mathbf {\dot {q}} ){\frac {\partial \mathbf {F} _{i}}{\partial s}}(\mathbf {Q} ,0)}$

• (FR) Marie Curie, Pierre Curie, Parigi, Éditions Dënoel, 1955. traduzione italiana CUEN, Napoli, 1998. L'edizione originale è del 1925.
• (FR) Pierre Curie, Sur la symétrie dans les phénomenes physiques, symétrie d'un champ eléctrique et d'un champ magnétique, in Journal de Physique, 3^me, serie 3, pp. 393-415.
• (DE) Ernst Haeckel, Kunstformen der Natur 1899-1904, Lipsia, Verlag des Bibliographischen Institut. URL consultato il 25 dicembre 2019 (archiviato dall'url originale il 27 giugno 2009).
• (EN) István Hargittai e Magdolna Hargittai, Symmetry Through the Eyes of a Chemist, 2ª ed., New York, Kluwer, 1995..
• (EN) István Hargittai e Magdolna Hargittai, In Our Own Image, New York, Kluwer, 2012, ISBN 978-14-61-36874-8.
• (EN) Ismael Jenann, Essays on Symmetry, New York, Garland, 2001, ISBN 978-08-15-33603-7.
• (EN) Alan Holden, Shapes, Space and Symmetry, Mineola, Dover Publications, 1992, ISBN 978-04-86-26851-4.
• (EN) A. Mouchet, Reflections on the four facets of symmetry: how physics exemplifies rational thinking, in European Physical Journal, H 38, 2013, p. 661.
• (EN) Joe Rosen, Symmetry Discovered, Londra, Cambridge University Press, 1975, ISBN 978-05-21-20695-2.
• (EN) Joe Rosen, A Symmetry Primer for Scientists, New York, John Wiley & Sons, 1983, ISBN 978-04-71-87672-4.
• (EN) Alexei Vasil'evich Shubnikov e Vladimir Alexandrovich Koptsik, Symmetry in Science and Art, New York, Plenum Press, 2012, ISBN 978-14-68-42069-2.
• (EN) Hermann Weyl, Symmetry, Princeton University Press, 1952, ISBN 0-691-02374-3.

• Chiralità (fisica)
• Derivata funzionale
• Equazioni di Hamilton
• Integrale funzionale
• Meccanica lagrangiana
• Modello standard
• Principio d'azione
• Rottura spontanea di simmetria
• Teorema di Nöther
• Teoria assorbitore-emettitore di Wheeler-Feynman

Portale Fisica: accedi alle voci di Teknopedia che trattano di fisica