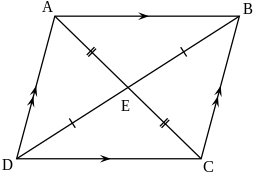
Per la geometria euclidea, un parallelogramma (o parallelogrammo) è un quadrilatero con i lati opposti paralleli. I lati e gli angoli opposti di un parallelogramma sono congruenti.
La congruenza dei lati e degli angoli opposti è una diretta conseguenza del V postulato di Euclide, relativo agli angoli interni determinati da una retta che ne taglia due, e nessuna delle caratteristiche del quadrilatero può essere dimostrata senza ricorrere al postulato di Euclide o a una delle sue formulazioni equivalenti.
L'etimologia, dal greco παραλληλ-όγραμμον, una forma "di linee parallele", riflette la definizione.
Il parallelogramma è un caso particolare di trapezio. Il parallelogramma ha due possibili altezze, secondo quale lato viene considerato come base.
Tipologie
[modifica | modifica wikitesto]- Quadrato - parallelogramma equilatero ed equi-angolo.
- Rettangolo - parallelogramma equiangolo.
- Rombo - parallelogramma equilatero.
- Romboide, parallelogramma che non è né un rombo né un rettangolo.
Dalle definizioni illustrate precedentemente è affermabile che:
- un quadrato è sempre sia un rettangolo che un rombo, mentre un rombo o un rettangolo non necessariamente sono quadrati.
Proprietà e criteri
[modifica | modifica wikitesto]- Un quadrilatero è un parallelogramma se e solo se le sue diagonali si bisecano, cioè ciascuna divide l'altra in due segmenti congruenti.
- Un quadrilatero è un parallelogramma se e solo se tutte le coppie di angoli interni consecutivi sono costituite da angoli supplementari.
- Un quadrilatero è un parallelogramma se e solo se le due coppie di angoli interni opposti sono costituite da angoli congruenti.
- Un quadrilatero è un parallelogramma se e solo se ha due lati opposti paralleli e congruenti.
La legge del parallelogramma caratterizza gli spazi di Hilbert nell'ambito degli spazi di Banach.
Ogni parallelogramma consente di costruire una tassellazione del piano.
La figura solida corrispondente tridimensionale del parallelogramma è il parallelepipedo.
Formula per l'area
[modifica | modifica wikitesto]
Un parallelogramma con base e altezza può essere diviso in un trapezoide e un triangolo retto, per essere ricombinato in un rettangolo, come mostrato nella figura a destra. Questo significa che l'area di un parallelogramma è la stessa di quella di un rettangolo con identica base e altezza:
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «parallelogramma»
Wikizionario contiene il lemma di dizionario «parallelogramma» Wikimedia Commons contiene immagini o altri file sul parallelogramma
Wikimedia Commons contiene immagini o altri file sul parallelogramma
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Melissa Petruzzello, parallelogram, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Parallelogramma, su MathWorld, Wolfram Research.
- (EN) Area of Parallelogram, su cut-the-knot.org.
- (EN) Equilateral Triangles On Sides of a Parallelogram, su cut-the-knot.org.
- (EN) Varignon Parallelogram, su cut-the-knot.org.
- (EN) Wittenbauer's Parallelogram, su cut-the-knot.org.
- (EN) Varignon and Wittenbauer Parallelograms by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
- (EN) Van Aubel's theorem Quadrilateral with four squares by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
- (EN) Parallelogram with five squares by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"












