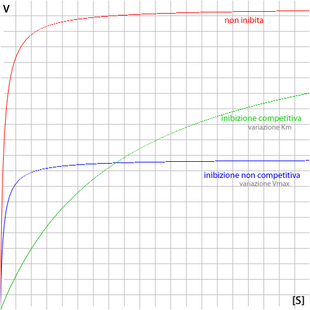
La cinetica di Michaelis-Menten descrive l'andamento della velocità di una reazione catalizzata da enzimi, al variare della concentrazione del substrato e dell'enzima. Questo modello, valido per enzimi non allosterici, fu proposto da Leonor Michaelis e Maud Menten nel 1913.^[1] Inibitori e induttori enzimatici sono sostanze in grado di alterare la cinetica enzimatica.

Il modello cinetico spiega come all'aumentare anche di poco della concentrazione del substrato disponibile all'enzima (di concentrazione supposta costante), la velocità della reazione aumenti fino al raggiungimento di un massimo, chiamato ${\displaystyle V_{max}}$. In questo punto la reazione ha raggiunto la velocità massima possibile semplicemente perché è presente tanto substrato da saturare tutto l'enzima presente in soluzione, perciò un'ulteriore aggiunta di substrato non servirebbe in quanto non verrebbe più attaccato da enzimi. Ciò avviene perché non sono più presenti enzimi liberi, ma solo forme enzimatiche legate al substrato.

L'enzima libero, indicato dalla lettera maiuscola ${\displaystyle E}$, reagisce dapprima con il substrato ${\displaystyle S}$ dando il complesso enzima-substrato ${\displaystyle ES}$, il quale si scomporrà originando il prodotto della reazione enzimatica, ${\displaystyle P}$, e riformando l'enzima libero.

Riassumendo schematicamente:^[2]

${\displaystyle E+S{\begin{matrix}k_{1}\\\longrightarrow \\\longleftarrow \\k_{-1}\end{matrix}}ES{\begin{matrix}k_{2}\\\longrightarrow \\\ \end{matrix}}E+P}$

dove i termini indicati con ${\displaystyle k}$ rappresentano le costanti specifiche di velocità di reazione. ES è un intermedio di reazione il cui basso valore di energia di attivazione permette di fare avvenire una specifica reazione, catalizzata da una specifica classe di enzimi, in modo molto favorevole (effetto catalitico). Quando ${\displaystyle ES}$, in seguito al raggiungimento di uno stato di equilibrio dinamico, assume un valore di concentrazione che si mantiene costante nel tempo, si dice che è stato raggiunto lo stato stazionario (steady state).^[3]

In condizioni di equilibrio la velocità di formazione del complesso enzima-substrato eguaglia la velocità di scomposizione:^[4]

${\displaystyle \operatorname {k} _{1}[E][S]=(k_{-1}+k_{2})[ES]}$

dove le parentesi quadre indicano la concentrazione molare.

La concentrazione totale dell'enzima, ${\displaystyle [E]_{0}}$ è eguale alla somma della concentrazione dell'enzima legato con la concentrazione dell'enzima libero:

${\displaystyle [E]+[ES]=[E]_{0}}$

Ricavando la concentrazione dell'enzima libero, ${\displaystyle [E]}$, da questa relazione e sostituendola nella espressione cinetica dello stato stazionario, precedentemente descritta, si ricava:

${\displaystyle \operatorname {k} _{1}([E]_{0}-[ES])[S]=(k_{-1}+k_{2})[ES]}$

dalla quale, eseguendo i prodotti, è possibile ottenere la concentrazione del complesso enzima-substrato ${\displaystyle [ES]}$, in funzione delle concentrazioni di substrato ed enzima totale:

${\displaystyle [ES]={\frac {k_{1}[E]_{0}[S]}{k_{1}[S]+k_{-1}+k_{2}}}}$

La velocità di formazione del prodotto è data dalla quantità di complesso enzima-substrato che si scompone in enzima libero e prodotto nell'unità di tempo:

${\displaystyle V=-{\frac {d[ES]}{dt}}=k_{2}[ES]=k_{2}{\frac {k_{1}[E]_{0}[S]}{k_{1}[S]+k_{-1}+k_{2}}}}$

Dividendo numeratore e denominatore del rapporto, per il termine k₁, si ottiene la nota equazione di Michaelis-Menten:

${\displaystyle V={\frac {k_{2}[E]_{0}[S]}{K_{M}+[S]}}}$

dove ${\displaystyle K_{M}}$ è la costante di Michaelis-Menten e rappresenta un termine che ingloba altri valori costanti.

Inoltre, visto che - una volta raggiunto lo stato stazionario - il valore della velocità massima ${\displaystyle V_{max}}$è dato dal prodotto ${\displaystyle V_{max}=k_{2}[E]_{0}}$, l'equazione di Michaelis-Menten può anche essere espressa nella forma alternativa:^[2]

${\displaystyle V={\frac {V_{max}[S]}{K_{M}+[S]}}}$

L'equazione di Michaelis e Menten mette quindi in relazione la velocità di formazione del prodotto ${\displaystyle V}$ con la concentrazione del substrato ${\displaystyle [S]}$.

Lo stesso argomento in dettaglio: Costante di Michaelis-Menten.

La costante di Michaelis-Menten, ${\displaystyle K_{M}}$, è una grandezza caratteristica di ciascun enzima.

Per un'equazione a due tappe del tipo ${\textstyle E+S\;{\underset {k_{-1}}{\overset {k_{1}}{\rightleftarrows }}}\;ES\;{\overset {k_{2}}{\rightarrow }}\;E+P}$, essa equivale al seguente rapporto ${\displaystyle K_{M}={\frac {k_{-1}+k_{2}}{k_{1}}}}$

In questa condizione, essendo ${\displaystyle k_{2}}$la tappa che limita la velocità, troviamo che ${\displaystyle k_{2}}$<< ${\displaystyle k_{-1}}$

${\displaystyle K_{M}}$ si ridurrà a ${\displaystyle k_{-1}/k_{1}}$ rappresentando quindi, a livello quantitativo l'affinità tra l'enzima e il substrato: più basso è il valore di K_M e più bassa sarà la concentrazione di substrato che permette di raggiungere un valore di velocità di reazione pari alla metà della velocità massima, il che indica una alta affinità dell'enzima per il substrato. Viceversa un alto valore di K_M indica che sarà necessario più substrato per raggiungere una velocità di reazione pari alla metà della velocità massima, il che significa una minore affinità dell'enzima per il substrato.

Per un'equazione a più di due tappe in cui alla formazione del complesso ${\displaystyle ES}$ seguono svariate reazioni, la ${\displaystyle K_{M}}$ diventa una funzione molto complessa di numerose costanti di velocità e non può quindi essere considerata una misura dell'affinità enzima-substrato.

Ragionando sull'equazione di Michaelis-Menten si ricava che la ${\displaystyle K_{M}}$ rappresenta, numericamente, la concentrazione di substrato necessaria affinché la reazione abbia velocità pari a metà della velocità. massima:

Per ${\displaystyle V_{0}=1/2V_{max}}$

${\displaystyle {V_{max} \over 2}={V_{max}[S] \over K_{m}+[S]}}$ ; ${\displaystyle {1 \over 2}={[S] \over K_{m}+[S]}}$  ;

risolvendo per ${\displaystyle K_{M}}$

${\displaystyle K_{m}+[S]=2[S]\longrightarrow K_{m}=[S]}$

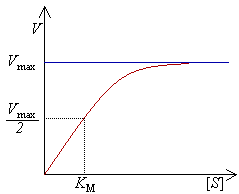
Riportando su un diagramma cartesiano l'andamento della velocità di reazione, dedotta secondo la cinetica di Michaelis-Menten, in funzione della concentrazione di substrato si ottiene graficamente un ramo di iperbole.

Risultano di ovvia deduzione le seguenti considerazioni:

• a basse concentrazioni di substrato la reazione è praticamente del primo ordine, crescendo la velocità proporzionalmente a [S] (essendo l'enzima in forte eccesso rispetto al substrato, la sua concentrazione può considerarsi costante);
• ad alte concentrazioni di substrato la velocità tende ad assumere un valore massimo che diviene costante. Ciò è dovuto alla completa saturazione dell'enzima che annulla l'effetto dovuto all'ulteriore aumento della concentrazione di substrato (non è presente più enzima disponibile). Una tale cinetica di reazione è di ordine zero e in questo caso risulta ${\displaystyle V_{max}=K_{2}[E]_{0}}$.

Riportando l'equazione di Michaelis-Menten nella forma:

${\displaystyle {\frac {1}{V}}={\frac {K_{M}}{V_{max}[S]}}+{\frac {1}{V_{max}}}}$

è possibile ottenere il grafico dei doppi reciproci (o di Lineweaver-Burk), rappresentando graficamente l'andamento di 1/V in funzione di 1/[S]. In tal modo si ottiene una retta con intercetta sull'asse delle ascisse nel punto - 1/K_M, sull'asse delle ordinate nel punto 1/V_max e con coefficiente angolare pari al rapporto K_M/V_max.

Quello dei doppi reciproci non è però l'unico grafico utile per interpretare la cinetica enzimatica, altri sono:

• grafico lineare diretto (o di Eisental-Cornish Bowden): V sulle ordinate e [S] sulle ascisse;
• grafico di Eadie-Hofstee: V sulle ordinate e V/[S] sulle ascisse;
• grafico di Hanes-Woolf: [S]/V sulle ordinate e [S] sulle ascisse.

• Luis Arnaut, Sebastiao Formosinho; Hugh Borrows, Chemical Kinetics - From Molecular Structure to Chemical Reactivity, Elsevier, 2007, ISBN 0-444-52186-0.
• David L. Nelson e Michael M. Cox. I principi di biochimica di Lehninger. IV edizione. Bologna, Zanichelli, 2006. ISBN 978-88-08-19774-0

• Catalisi enzimatica
• Costante di Michaelis-Menten
• IC50
• Inibitore enzimatico
• Diagramma di Lineweaver-Burk

• Wikimedia Commons contiene immagini o altri file sulla cinetica di Michaelis-Menten

• (EN) Michaelis-Menten kinetics, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.

Portale Biologia

Portale Chimica

Portale Fisica