Indice
Meccanica del contatto con attrito
La meccanica del contatto è lo studio della deformazione di solidi che si toccano in uno o più punti.[1][2] Questo può essere diviso in forze compressive e adesive in direzione perpendicolare all'interfaccia, e in forze di attrito in direzione tangenziale. La meccanica del contatto con attrito (o contatto frizionale) è lo studio della deformazione dei corpi in presenza di effetti di attrito, mentre la meccanica del contatto senza attrito assume l'assenza di tali effetti.
La meccanica del contatto senza attrito si occupa di un'ampia gamma di scale diverse.
- Su scala macroscopica, essa si applica all'indagine sul moto dei corpi in contatto (vedi Dinamica del contatto). Ad esempio il rimbalzo di una palla di gomma su una superficie dipende dall'interazione degli attriti sull'interfaccia di contatto. Qui sono di interesse principale la forza totale rispetto all'indentazione e allo spostamento laterale.
- Su scala intermedia, si è interessati alle tensioni, agli allungamenti e alle deformazioni locali dei corpi in contatto nella e vicino all'area di contatto. Ad esempio per derivare o validare i modelli di contatto su scala macroscopica, o per indagare l'usura e la fatica delle superfici dei corpi in contatto. Le aree di applicazione di questa scala sono l'interazione pneumatico-pavimentazione, l'interazione ruota ferroviaria-rotaia, l'analisi dei cuscinetti a rulli, ecc.
- Infine, su scala microscopica e nanoscopica, la meccanica del contatto si usa per aumentare la nostra comprensione dei sistemi tribologici, ad es. indagare l'origine dell'attrito, e per l'ingegneria di dispositivi avanzati come i microscopi a forza atomica e i dispositivi MEMS.
Questo articolo si occupa principalmente della seconda scala: ottenere la comprensione basilare delle tensioni e delle deformazioni nella e vicino alla zona di contatto, senza prestare troppa attenzione ai meccanismi dettagliati mediante i quali essi avvengono.
Storia
[modifica | modifica wikitesto]Parecchi famosi scienziati e ingegneri hanno contribuito alla nostra comprensione dell'attrito.[3] Essi includono Leonardo da Vinci, Guillaume Amontons, John Theophilus Desaguliers, Leonhard Euler e Charles-Augustin de Coulomb. In seguito, Nikolai Pavlovich Petrov, Osborne Reynolds e Richard Stribeck completarono questa conoscenza con le teorie della lubrificazione.
La deformazione dei materiali solidi fu indagata nel XVII e XVIII secolo da Robert Hooke, Joseph Louis Lagrange, e nel XIX e XX secolo da d'Alembert e Timoshenko. Rispetto alla meccanica del contatto spicca il contributo classico di Heinrich Hertz.[4] Inoltre le soluzioni fondamentali di Boussinesq e Cerruti sono di primaria importanza per l'indagine dei problemi di contatto con attrito nel regime (linearmente) elastico.
I risultati classici di un vero problema di contatto frizionale riguardano i saggi di F. W. Carter (1926) e H. Fromm (1927). Essi presentarono indipendentemente la reazione scivolamento verso forza di scivolamento per un cilindro su un piano o per due cilindri in contatto volvente stabile usando la legge dell'attrito secco di Coulomb (vedi sotto).[5] Questi si applicano alla trazione delle locomotive ferroviarie, e per la comprensione dell'oscillazione di serpeggiamento dei veicoli ferroviari. Rispetto allo scivolamento, le soluzioni classiche sono dovute a C. Cattaneo (1938) e a R. D. Mindlin (1949), che consideravano il cambio di velocità tangenziale di una sfera su un piano (vedi sotto).[1]
Negli anni 1950 crebbe l'interesse per il contatto volvente delle ruote ferroviarie. Nel 1958 K. L. Johnson presentò un approccio approssimato per il problema dell'attrito tridimensionale con la geometria hertziana, con scivolamento o laterale o rotatorio. Tra le altre cose trovò che lo scivolamento rotatorio, che è simmetrico intorno al centro della zona di contatto, conduce a una forza laterale netta in condizioni volventi. Ciò è dovuto alle differenze longitudinali nella distribuzione delle trazioni della zona di contatto.
Nel 1967 Joost Kalker pubblicò la sua miliare tesi di dottorato sulla teoria lineare per il contatto volvente.[6] Questa teoria è esatta per la situazione di un coefficiente di attrito infinito, nel qual caso l'area di slittamento scompare, ed è approssimativa per gli scivolamenti che non scompaiono. Essa assume la legge dell'attrito di Coulomb, che richiede più o meno superfici (scrupolosamente) pulite. Questa teoria è per corpi massicci come il contatto ruota ferroviaria-rotaia. Rispetto all'interazione strada-pneumatico, un contributo importante riguarda la cosiddetta formula magica degli pneumatici di Hans Pacejka.[7]
Negli anni 1970 furono messi a punto molti modelli numerici. Particolarmente gli approcci variazionali, come quelli che fanno affidamento sulle teorie dell'esistenza e dell'unicità di Duvaut e Lion. Nel tempo, queste si svilupparono in approcci degli elementi finiti per i problemi di contatto con i modelli e le geometrie generali dei materiali, e in approcci basati sui semispazi per i cosiddetti problemi di contatto con bordi levigati per i materiali linearmente elastici. I modelli della prima categoria furono presentati da Laursen[8] e da Wriggers.[9] Un esempio di quest'ultima categoria è il modello CONTACT di Kalker.[10]
Un inconveniente degli approcci variazionali ben fondati sono i loro grandi tempi di calcolo. Perciò furono escogitati anche molti diversi approcci approssimati. Varie e ben note teorie approssimate per il problema del contatto volvente sono l'approccio FASTSIM di Kalker, la formula di Shen-Hedrick-Elkins e l'approccio di Polach.
Altre informazioni sulla storia del problema del contatto ruota/rotaia sono forniti nel saggio di Knothe.[5] Inoltre Johnson raccolse nel suo libro un'enorme quantità di informazioni sulla meccanica del contatto e sugli argomenti correlati.[1] Rispetto alla meccanica del contatto volvente una panoramica delle varie teorie è presentata anche da Kalker.[11] Infine sono d'interesse gli atti di un corso della CISM, che forniscono un'introduzione ad aspetti più avanzati della teoria del contatto volvente.[12]
Formulazione del problema
[modifica | modifica wikitesto]Centrale nell'analisi dei problemi di contatto con attrito è la comprensione che le tensioni sulla superficie di ciascun corpo sono variabili spazialmente. Conseguentemente anche gli allungamenti e le deformazioni dei corpi sono variabili con la posizione. E il moto delle particelle dei corpi a contatto può essere diverso in punti diversi: in parte della zona di contatto le particelle dei corpi opposti possono aderire (attaccarsi) l'una all'altra, mentre in altre parti della zona di contatto avviene un movimento relativo. Questo scorrimento relativo locale è chiamato micro-deriva.
Questa suddivisione dell'area di contatto in aree di attaccatura (adesione) e aree di deriva si manifesta tra l'altro nell'usura corrosiva. Si noti che l'usura si verifica solo dove è dissipata potenza, il che richiede una tensione e uno spostamento relativo locale (deriva) tra le due superfici.
La dimensione e la forma della stessa zona di contatto e della e sue aree di adesione e di deriva non sono generalmente note in anticipo. Se fossero note, allora i campi elastici nei due corpi sarebbero risolti indipendentemente l'uno dall'altro e questo non sarebbe più un problema di contatto.
Tre diverse componenti possono essere distinte in un problema di contatto.
- Prima di tutto, c'è la deformazione dei corpi separati in reazione ai carichi applicati alle loro superfici. Questo è l'oggetto della meccanica del continuo generale. Esso dipende in gran parte dalla geometria dei corpi e dal comportamento dei loro materiali (costitutivi) (ad es. risposta elastica contro plastica, struttura omogenea contro stratificata, ecc.).
- In secondo luogo, c'è un moto complessivo dei corpi l'uno in relazione all'altro. Ad esempio i corpi possono essere in quiete (statica) o in rapido avvicinamento tra loro (impatto), e possono essere spostati (scorrimento) o ruotati (rotolamento) l'uno sull'altro. Questi moti complessivi sono studiati nella meccanica classica, vedi ad esempio la dinamica multicorpo.
- Infine ci sono i processi sull'interfaccia di contatto: compressione e adesione nella direzione perpendicolare all'interfaccia, e attrito e micro-deriva nelle direzioni tangenziali.
L'ultimo aspetto è l'oggetto primario della meccanica del contatto. È descritto in termini delle cosiddette "condizioni di contatto". Per la direzione perpendicolare all'interfaccia, il problema di contatto normale, gli effetti di adesione sono solitamente piccoli (sulle scale spaziali maggiori) e si impiegano tipicamente le seguenti condizioni:
- Il divario tra le due superfici deve essere zero (contatto) o strettamente positivo (separazione, );
- La tensione normale che agisce su ciascun corpo è zero (separazione) o compressiva ( nel contatto).
Matematicamente: . Qui sono funzioni che variano con la posizione lungo le superfici dei corpi.
Nelle direzioni tangenziali si usano spesso le seguenti condizioni:
- Lo sforzo di taglio locale (tangenziale) (assumendo la direzione normale parallela all'asse ) non può superare il massimo dipendente da una certa posizione, il cosiddetto limite di trazione ;
- Dove l'ampiezza della trazione tangenziale ricade al di sotto del limite di trazione , le superfici opposte aderiscono insieme e la microderiva scompare, ;
- La microderiva si verifica dove le trazioni tangenziali sono al limite di trazione; la direzione della trazione tangenziale è allora opposta alla direzione della microderiva .
La forma precisa del limite di trazione è la cosiddetta legge dell'attrito locale. Per questo la legge dell'attrito (globale) di Coulomb è spesso applicata localmente: , con il coefficiente di attrito. Sono possibili anche formule più dettagliate, per esempio con a seconda della temperatura , della velocità di scorrimento locale , ecc.
Soluzioni per i casi statici
[modifica | modifica wikitesto]Corda su una bitta, l'equazione del cabestano
[modifica | modifica wikitesto]
Si consideri una corda in cui forze uguali (ad es. ) sono esercitate su entrambi i lati. In questo modo la corda è leggermente tesa e si induce una tensione interna ( su ogni posizione lungo la corda). La corda è avvolta intorno a un elemento fisso come una bitta; è piegata ed è a contatto con la superficie dell'elemento con un angolo di contatto (ad es. ). Tra la corda e la bitta si genera una pressione normale, ma non si presenta ancora nessun attrito. Poi la forza su un lato della bitta è aumentata a un valore superiore (e.g. ). Questo causa sforzi di taglio frizionali nell'area di contatto. Nella situazione finale la bitta esercita una forza di attrito sulla corda tale da determinare una situazione statica.
La distribuzione delle tensioni nella corda in questa situazione finale è descritta dall'equazione del cabestano, con soluzione:
La tensione aumenta da sul lato lento () a sul lato alto . Quando si guarda dal lato alto, la tensione cala esponenzialmente, finché raggiunge il carico minore a . Da là in poi essa è costante a questo valore. Il punto di transizione è determinato dal rapporto tra i due carichi e il coefficiente di attrito. Qui le tensioni sono in newton e gli angoli in radianti.
La tensione nella corda nella situazione finale è aumentata rispetto allo stato iniziale. Perciò la corda si è leggermente allungata. Questo significa che non tutte le particelle superficiali della corda possono aver mantenuto la loro posizione iniziale sulla superficie della bitta. Durante il processo di caricamento, la corda è scivolata leggermente lungo la superficie nell'area di scivolamento (slip area) . Questo scivolamento è precisamente abbastanza largo da arrivare all'allungamento che si verifica nello stato finale. Si noti che non c'è scivolamento che avviene nello stato finale; il termine area di scivolamento si riferisce allo scorrimento (slippage) che si è verificato durante il processo di caricamento. Si noti ancora che la localizzazione dell'area di scivolamento dipende dallo stato iniziale e dal processo di caricamento. Se la tensione iniziale è e la tensione è ridotta a nel lato lento, allora l'area di scivolamento si verifica nel lato lento dell'area di contatto. Per le tensioni iniziali fra e , ci possono essere aree di scivolamento su entrambi i lati con un'area di adesione in mezzo.
Sfera su un piano, il problema (tridimensionale) di Cattaneo
[modifica | modifica wikitesto]Si consideri una sfera che è premuta su un piano (semispazio) e poi spostata sulla superficie del piano. Se la sfera e il piano sono visti idealmente come corpi rigidi, allora il contatto si verificherebbe esattamente in un unico punto, e la sfera non si muoverebbe fino a quando la forza tangenziale che è applicata non raggiunge la forza di attrito massima. Allora la sfera inizia a scivolare sulla superficie fino a quando la forza applicata non è di nuovo ridotta.
In realtà, con gli effetti elastici presi in considerazione, la situazione è molto diversa. Se una sfera elastica è premuta su un piano elastico dello stesso materiale, allora entrambi i corpi si deformano, si crea un'area circolare e sorge una distribuzione normale (hertziana) della pressione. Inoltre, il centro della sfera è spostato leggermente verso il basso di una distanza che è chiamata l'approccio, che è anche la massima penetrazione delle superfici indeformate. Per una sfera di raggio e costanti elastiche la soluzione hertziana recita:
Si consideri ora che è applicata una forza tangenziale che è inferiore al limite dell'attrito di Coulomb . Il centro della sfera sarà allora spostato lateralmente di una piccola distanza che è chiamata spostamento. Si ottiene un equilibrio statico nel quale si verificano deformazioni elastiche nonché sforzi di taglio frizionali nell'interfaccia di contatto. In questo caso, se la forza tangenziale si riduce, allora anche le deformazioni elastiche e gli sforzi di taglio si riducono. La sfera ritorna in gran parte nella sua posizione originaria, tranne per le perdite di attrito che sorgono a causa dello scivolamento locale nell'area di contatto.
Questo problema di contatto fu risolto in modo approssimato da Cattaneo usando un approccio analitico. La distribuzione degli sforzi nello stato di equilibrio consiste di due parti:
Nella regione centrale, adesiva, , le particelle superficiali del piano si spostano lungo verso destra mentre le particelle superficiali della sfera si spostano lungo verso sinistra. Anche se la sfera nell'insieme si muove lungo rispetto al piano, queste particelle superficiali non si sono mosse l'una rispetto all'altra. Nell'anello circolare esterno , le particelle superficiali invece si sono mosse l'una rispetto all'altra. Il loro spostamento locale si ottiene come
Questo spostamento ha esattamente una grandezza tale, che si ottiene un equilibrio statico con sforzi di taglio al limite di trazione in questa cosiddetta area di scivolamento (slip area).
Così, durante il caricamento tangenziale della sfera, si verifica uno scorrimento parziale. L'area di contatto è divisa in tal modo in un'area di scivolamento dove le superfici si muovono l'una rispetto all'altra e in un'area di adesione dove non si muovono. Nello stato di equilibrio, non avviene più alcuno scorrimento.
Soluzioni per i problemi di scorrimento dinamico
[modifica | modifica wikitesto]La soluzione di un problema di contatto consiste nello stato sull'interfaccia (dov'è il contatto, la divisione dell'area di contatto in zone di adesione e in zone di scivolamento e le distribuzioni normali e dello sforzo di taglio) più il campo elastico all'interno dei corpi. Questa soluzione dipende dalla storia del contatto. Ciò può essere visto mediante un'estensione del problema di Cattaneo descritto sopra.
- Nel problema di Cattaneo, la sfera è dapprima premuta sul piano e poi spostata tangenzialmente. Questo produce uno scivolamento parziale come descritto sopra.
- Se la sfera è dapprima spostata tangenzialmente e poi premuta sul piano, allora non c'è alcuna differenza di spostamento tra le superfici opposte e conseguentemente non c'è alcuna tensione tangenziale nell'interfaccia di contatto.
- Se l'avvicinamento in direzione normale e lo spostamento tangenziale sono aumentati simultaneamente ("compressione obliqua"), allora si può ottenere una situazione con tensione tangenziale ma senza scivolamento locale.[2]
Questo dimostra che lo stato nell'interfaccia di contatto non è dipendente solo dalle posizioni relative dei due corpi, ma anche dalla storia del loro moto. Un altro esempio di ciò si verifica se la sfera è riportata nella sua posizione originaria. Inizialmente non c'era alcuna tensione tangenziale nell'interfaccia di contatto. Dopo si è verificato il micro-scivolamento iniziale. Questo micro-scivolamento non si annulla interamente spostandosi indietro. Perciò, nella situazione finale rimangono tensioni tangenziali nell'interfaccia, in quella che sembra una configurazione identica a quella originaria.
Soluzione dei problemi di contatto con rotolamento
[modifica | modifica wikitesto]
I problemi di contatto con rotolamento sono problemi dinamici nei quali i corpi a contatto sono in continuo movimento l'uno rispetto all'altro. Una differenza con i problemi di contatto con scorrimento dinamico è che c'è maggiore varietà nello stato delle diverse particelle superficiali. Mentre la zona di contatto in un problema di scorrimento consiste continuamente più o meno delle stesse particelle, in un problema di contatto con rotolamento le particelle entrano ed escono dalla zona di contatto incessantemente. Inoltre, in un problema di scorrimento le particelle superficiali sono tutte soggette ovunque più o meno allo stesso spostamento tangenziale, mentre in un problema di rotolamento le particelle superficiali sono sollecitate in modi piuttosto diversi. Esse sono libere da sollecitazioni quando entrano nella zona di contatto, poi aderiscono a una particella della superficie opposta, sono deformate dalla differenza del moto complessivo tra i due corpi, finché non si raggiunge il limite di trazione locale e inizia lo scivolamento locale. Questo processo è in stadi diversi per le diverse parti dell'area di contatto.
Se il moto complessivo dei corpi è costante, allora si può conseguire uno stato stazionario complessivo. Qui lo stato di ciascuna particella superficiale varia nel tempo, ma la distribuzione complessiva può essere costante. Ciò si formalizza usando un sistema di coordinate che si muove lungo la zona di contatto.
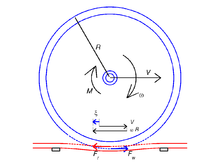
Rotolamento di un cilindro su un piano, la soluzione (bidimensionale) di Carter-Fromm
[modifica | modifica wikitesto]Si consideri un cilindro che rotola su un piano (semispazio) in condizioni stazionarie, con uno scivolamento longitudinale indipendente dal tempo. (Relativamente) lontano dalle estremità dei cilindri si verifica una situazione di deformazione piana e il problema è bidimensionale.
Se il cilindro e il piano consistono degli stessi materiali, allora il problema del contatto normale è insensibile allo sforzo di taglio. L'area di contatto è una striscia , e la pressione è descritta dalla soluzione bidimensionale di Hertz.
La distribuzione dello sforzo di taglio dalla soluzione di Carter-Fromm. Consiste di un'area di adesione al bordo di entrata dell'area di contatto e di un'area di scivolamento al bordo di uscita. La lunghezza dell'area di adesione è denotata . Inoltre la coordinata di adesione è introdotta da . Nel caso di una forza positiva (scivolamento negativo ) è:
La dimensione dell'area di adesione dipende dallo scivolamento, dal raggio della ruota e dal coefficiente di attrito.
Per scivolamenti maggiori tali che si verifica uno scivolamento completo.
Approcci basati sui semispazi
[modifica | modifica wikitesto]Quando si considerano i problemi di contatto su scale spaziali intermedie, le disomogeneità dei materiali e la rugosità delle superfici rilevabili su scala ridotta si ignorano. I corpi si considerano formati da superfici levigate e materiali omogenei. Si assume un approccio continuo nel quale le tensioni, le deformazioni e gli spostamenti sono descritti da funzioni (parzialmente) continue.
L'approccio dei semispazi è un'elegante strategia risolutiva per i cosiddetti problemi di contatto con "bordi levigati" o "concentrati".
- Se un corpo elastico massivo è caricato su una piccola sezione della sua superficie, allora le tensioni elastiche si attenuano proporzionalmente a e gli spostamenti elastici di quando ci si muove lontano da quest'area superficiale.
- Se un corpo non ha spigoli vivi nella o vicino alla regione di contatto, allora la sua risposta a un carico superficiale può essere ben approssimata dalla risposta di un semispazio elastico (ad es. tutti i punti con ).
- Il problema del semispazio elastico è risolto analiticamente, vedi la soluzione di Boussinesq-Cerruti.
- A causa della linearità di questo approccio, possono essere sovrapposte molteplici soluzioni parziali.
Usando la soluzione fondamentale per il semispazio, il problema completo del contatto tridimensionale è ridotto a un problema bidimensionale per le superfici delimitanti dei corpi.
Un'ulteriore semplificazione si verifica se i due corpi sono "geometricamente ed elasticamente simili". In generale, la tensione all'interno di un corpo in una certa direzione induce spostamenti anche nelle direzioni perpendicolari. Conseguentemente, nel problema di contatto c'è un'interazione tra la tensione normale e gli spostamenti tangenziali, e un'interazione fra la tensione tangenziale e gli spostamenti normali. Ma se la tensione normale nell'interfaccia di contatto induce gli stessi spostamenti tangenziali in entrambi i corpi a contatto, allora non c'è nessuno spostamento tangenziale relativo delle due superfici. In quel caso, i problemi di contatto normale e tangenziale sono disaccoppiati. Se questo avviene, allora i due corpi sono chiamati quasi identici. Ciò accade ad esempio se i corpi sono simmetrici speculari rispetto al piano di contatto e hanno le stesse costanti elastiche.
Le soluzioni classiche basate sull'approccio dei semispazi sono:
- Hertz risolse il problema del contatto in assenza di attrito, per una geometria semplice (superfici curve con raggi di curvatura costanti).
- Carter considerò il contatto con rotolamento tra un cilindro e un piano, come descritto sopra. Una soluzione analitica completa è fornita per la trazione tangenziale.
- Cattaneo considerò la compressione e lo spostamento di due sfere, come descritto sopra. Si noti che questa soluzione analitica è approssimata. In realtà si verificano piccole trazioni tangenziali che sono ignorate.
Note
[modifica | modifica wikitesto]- ^ a b c K.L. Johnson, Contact Mechanics, Cambridge, Cambridge University Press, 1985.
- ^ a b V.L. Popov, Contact Mechanics and Friction. Physical Principles and Applications, Berlino, Springer-Verlag, 2010.
- ^ Introduction to Tribology – Friction, su depts.washington.edu. URL consultato il 21 dicembre 2008.
- ^ Heinrich Hertz, Contact between solid elastic bodies, in Journ. für reine und angewandte Math., vol. 92, 1882.
- ^ a b K. Knothe, History of wheel/rail contact mechanics: from Redtenbacher to Kalker, in Vehicle System Dynamics, vol. 46, n. 1-2, 2008, pp. 9–26.
- ^ Joost J. Kalker, On the rolling contact of two elastic bodies in the presence of dry friction, Delft University of Technology, 1967.
- ^ Hans Pacejka, Tire and Vehicle Dynamics, Oxford, Butterworth-Heinemann, 2002.
- ^ T. A. Laursen, Computational Contact and Impact Mechanics, Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis, Berlino, Springer, 2002.
- ^ P. Wriggers, Computational Contact Mechanics, 2nd ed., Heidelberg, Springer, 2006.
- ^ J. J. Kalker, Three-Dimensional Elastic Bodies in Rolling Contact, Dordrecht, Kluwer Academic Publishers, 1990.
- ^ J. J. Kalker, Three-Dimensional Elastic Bodies in Rolling Contact, Dordrecht, Kluwer Academic Publishers, 1990.
- ^ B. Jacobsen e J.J. Kalker (a cura di), Rolling Contact Phenomena, Vienna-New York, Springer-Verlag, 2000.
Voci correlate
[modifica | modifica wikitesto]Collegamenti esterni
[modifica | modifica wikitesto]- (EN) [1][collegamento interrotto] Biografia di J. J. Kalker (Università tecnica di Delft).
- (EN) [2] Programma CONTACT hertziano/non hertziano di Kalker.
































![{\displaystyle {\begin{matrix}T(\phi )=T_{hold},&\phi \in [\phi _{hold},\phi _{intf}]\\T(\phi )=T_{load}\exp(-\mu \phi ),&\phi \in [\phi _{intf},\phi _{load}]\\\phi _{intf}=\log(T_{load}/T_{hold})/\mu &\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b4217138d9d35959ceb01ec42b3d185640e529c)







![{\displaystyle \phi \in [\phi _{intf},\phi _{load}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab3ee1834c387e8272924728de2d82116d2b589)

















![{\displaystyle x\in [-a,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/230fb811e68a2cb420107a2a6bbf81d435385aff)












