Tetraemiesaedro
| Tetraemiesaedro | |||
|---|---|---|---|
 | |||
| Tipo | Poliedro stellato uniforme | ||
| Forma facce | 4 triangoli 3 quadrati | ||
| Nº facce | 7 | ||
| Nº spigoli | 12 | ||
| Nº vertici | 6 | ||
| Caratteristica di Eulero | 1 | ||
| Incidenza dei vertici | 4.3/2.4.3 | ||
| Notazione di Wythoff | 3/2 3 | 2 | ||
| Diagramma di Coxeter-Dynkin | |||
| Gruppo di simmetria | Td, [3,3], *332 | ||
| Duale | Tetraemiesacrono | ||
| Proprietà | Non convessità | ||
| Politopi correlati | |||
| |||
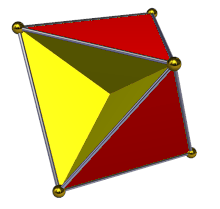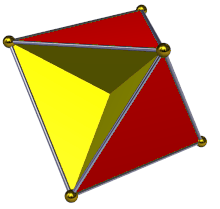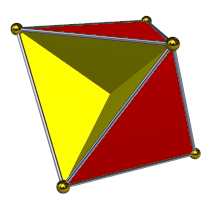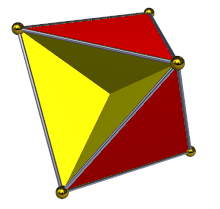
In geometria, un tetraemiesaedro, spesso indicato anche come emicubottaedro, è un poliedro stellato uniforme, e in particolare un emipoliedro, avente 7 facce - 4 triangolari e 3 quadrate - 12 spigoli e 6 vertici.
Proprietà
[modifica | modifica wikitesto]La figura al vertice di questo poliedro, che viene spesso indicato con il simbolo U4 e che è l'unico poliedro uniforme non-prismatico ad avere un numero dispari di facce, è un quadrilatero incrociato.[1]
Utilizzando la notazione di Wythoff, il tetraemiesaedro può essere indicato come "3/2 3 | 2", mentre il suo diagramma di Coxeter-Dynkin è ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Come detto, il tetraemiesaedro appartiene all'insieme degli emipoliedri, ossia poliedri stellati uniformi aventi alcune delle facce passanti per il proprio centro e così chiamati perché in essi tali facce formano un gruppo contenente la metà degli stessi elementi presenti in un poliedro regolare e disposti come in esso, da cui il prefisso "emi-". In particolare, nel tetraemiesaedro tale gruppo è formato dalle sue tre facce quadrate, che sono orientate nella stessa direzione delle facce di un esaedro (altro nome con cui si indica il cubo), che sono mutualmente perpendicolari e che passano per il suo centro. Va notato che, visivamente, ognuna di tali facce quadrate è divisa in quattro triangoli rettangoli, visibili a coppie su lati opposti del solido.
Poliedri correlati
[modifica | modifica wikitesto]Il tetraemiesaedro ha gli stessi vertici e gli stessi spigoli di un ottaedro regolare, con cui ha in comune anche 4 facce triangolari e da cui lo differenzia la presenza di tre facce quadrate passanti per il suo centro.
 Ottaedro |
 Tetraemiesaedro |
Il tetraemiesaedro è poi 2-rivestito da un cubottaedro, che ha quindi la stessa figura al vertice astratta (due triangoli e due quadrati: 3.4.3.4) e un numero doppio di vertici, spigoli e facce.
 Cubottaedro |
 Tetraemiesaedro |
Questo poliedro può anche essere costruito come una semicupola (o cupoloide), essendo una versione della cupola triangolare retrograda, {3⁄2}-cupola, a cui viene sottratta la base {6⁄2}-gonale.
| n⁄d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  Semicupola triangolare incrociata |
 Semicupola pentagrammica |
 Semicupola eptagrammica |
| 4 | — |  Semicupola pentagonale incrociata |
 Semicupola eptagrammica incrociata |
Tetraemiesacrono
[modifica | modifica wikitesto]| Tetraemiesacrono | |
|---|---|
 | |
| Tipo | Poliedro stellato |
| Nº facce | 6 |
| Nº spigoli | 12 |
| Nº vertici | 7 |
| Caratteristica di Eulero | 1 |
| Gruppo di simmetria | Td, [3,3], *332 |
| Duale | Tetraemiesaedro |
Il tetraemiesacrono è il duale del tetraemiesaedro, nonché uno dei 9 emipoliedri duali esistenti.
Poiché gli emipoliedri hanno facce passanti per il loro centro, i loro duali hanno vertici posti all'infinito, e più precisamente all'infinito sul piano proiettivo reale.[2] Nella sua opera "Dual Models", Magnus Wenninger rappresenta tali figure come prismi intersecanti, ognuno dei quali si estende all'infinito verso il vertice stesso, così da mantenere la simmetria. Nella comune rappresentazione i prismi costituenti il modello vengono per comodità tagliati a un certo punto della loro altezza. Wenninger ha suggerito di inserire queste nuove figure in una nuova classe di solidi generati per stellazione, chiamati "stellazioni all'infinito". Tuttavia egli ha anche affermato che, strettamente parlando, tali figure non sarebbero in effetti poliedri poiché la loro costruzione non risulta conforme alle comuni definizioni.[2]
Topologicamente, si considera che il tetraemiesacrono contenga sette vertici. I tre vertici considerati all'infinito (sul piano proiettivo reale all'infinito) corrispondono ai tre vertici dell'emiottaedro, un poliedro astratto, mentre gli altri quattro vertici sono presenti ai quattro angoli alternati di un cubo centrale (un demicubo, in questo caso un tetraedro).
Note
[modifica | modifica wikitesto]- ^ David A. Richter, Two Models of the Real Projective Plan, Western Michigan University. URL consultato il 2 maggio 2022 (archiviato dall'url originale il 3 marzo 2016).
- ^ a b Magnus Wenninger, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 730208.
Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su Tetraemiesaedro
Wikimedia Commons contiene immagini o altri file su Tetraemiesaedro
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Eric W. Weisstein, Tetraemiesaedro, su MathWorld, Wolfram Research.










