Funzione di Cantor

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

---

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

In matematica, la funzione di Cantor (a volte chiamata funzione di Cantor-Vitali, o scala del diavolo) è un esempio di funzione continua e crescente con derivata zero in quasi tutti i punti essendo costante in tutti i sottointervalli di ${\displaystyle [0,1]}$ che non contengono punti dell'insieme di Cantor.

Intuitivamente, è una scala con infiniti gradini, tutti di pendenza zero, ma ad altezze progressivamente crescenti, in modo che la pendenza media risulti comunque pari a ${\displaystyle 1}$.

La funzione di Cantor ${\displaystyle f\colon [0,1]\rightarrow [0,1]}$ è definita nel modo seguente:

1. Scriviamo ogni numero ${\displaystyle x\in [0,1]}$ in base tre. Con questa notazione: ${\displaystyle 1/3=0,1_{3},}$ e ${\displaystyle 2/3=0,2_{3}}$. Notiamo che alcuni numeri razionali possono avere due scritture diverse, ad esempio ${\displaystyle 1/3=0,0222\ldots _{3}}$ (questo fatto è vero anche in base 10: infatti ${\displaystyle 0,1=0,09999\ldots }$). Scegliamo, quando è possibile, una notazione che non contiene la cifra ${\displaystyle 1}$.
2. Sostituiamo la prima occorrenza della cifra ${\displaystyle 1}$ con un ${\displaystyle 2}$ e tutte le cifre successive con ${\displaystyle 0}$.
3. Sostituiamo tutte le cifre ${\displaystyle 2}$ con ${\displaystyle 1}$.
4. Interpretiamo il risultato come un numero binario. Questo risultato è ${\displaystyle f(x)}$.

Ad esempio:

• ${\displaystyle 1/4=0,02020202\ldots _{3}\mapsto 0,01010101_{2}=1/3}$. Quindi ${\displaystyle f(1/4)=1/3}$.
• ${\displaystyle 1/5=0,01210121\ldots _{3}}$, al passo 2 diventa ${\displaystyle 0,02000000\ldots }$, quindi ${\displaystyle 0,01000000\ldots _{2}=1/4}$. Quindi ${\displaystyle f(1/5)=1/4}$.

La funzione si può anche definire come limite di una successione di funzioni definite in ${\displaystyle [0,1]}$, costruite in questo modo:

• Sia ${\displaystyle f_{0}(x)=x}$.
• Sia ${\displaystyle f_{n}(x)}$ una funzione crescente il cui grafico è la poligonale suggerita in figura a lato, avente ${\displaystyle 2^{n+1}-1}$ lati: ${\displaystyle 2^{n}}$ lati sono obliqui di coefficiente angolare ${\displaystyle (3/2)^{n}}$ e ${\displaystyle 2^{n}-1}$ lati sono orizzontali, ciascuno di lunghezza ${\displaystyle \left({\frac {1}{3}}\right)^{n}}$. Per ogni ${\displaystyle n}$ intero non negativo risulta ${\displaystyle f_{n}(0)=0}$ e ${\displaystyle f_{n}(1)=1}$. In figura sono disegnate ${\displaystyle f_{0}}$, ${\displaystyle f_{1}}$ e ${\displaystyle f_{2}}$.

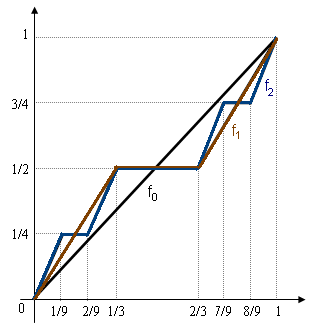
Si può "costruire" la ${\displaystyle (n+1)}$-esima poligonale ${\displaystyle f_{n+1}}$ come una trasformazione della ${\displaystyle f_{n}}$: infatti, dette ${\displaystyle I_{k}^{(n)},}$ per ${\displaystyle k=1,\ldots ,2^{n},}$ e ${\displaystyle J_{k}^{(n)},}$ per ${\displaystyle k=1,\ldots ,2^{n}-1,}$ le proiezioni sull'asse delle ascisse dei lati obliqui e di quelli orizzontali rispettivamente (notare che è ${\displaystyle f(J_{k}^{(n)})=k/2^{n}}$), allora è ${\displaystyle f_{n+1}=f_{n}}$ in ${\displaystyle J_{k}^{(n)}}$ per ogni ${\displaystyle k}$, mentre ogni lato obliquo di ${\displaystyle f_{n}}$ (che ha come proiezione sull'asse delle ascisse l'intervallo ${\displaystyle I_{k}^{(n)}}$) viene modificato in tre lati, di cui due obliqui in corrispondenza agli intervalli ${\displaystyle I_{2k-1}^{(n+1)}}$ e ${\displaystyle I_{2k}^{(n+1)}}$, e uno orizzontale in corrispondenza all'intervallo ${\displaystyle J_{2k-1}^{(n+1)}}$.

Si può dimostrare che risulta:

${\displaystyle \sup _{p\in \mathbb {N} \ }\left\{\max _{x\in [0,1]}\{f_{n}(x)-f_{n+p}(x)\}\right\}\leq {\frac {1}{3\cdot 2^{n}}}.}$

Da quest'ultimo risultato ne viene che tale successione è di Cauchy nello spazio delle funzioni continue in ${\displaystyle [0,1]}$. Dunque per ${\displaystyle n\to \infty }$ converge uniformemente ad una funzione limite, che è detta funzione di Cantor.

La funzione di Cantor è una funzione continua (in quanto limite uniforme di funzioni continue), crescente e suriettiva dall'intervallo ${\displaystyle [0,1]}$ in sé. È a variazione limitata ma non assolutamente continua. Non è derivabile in nessun punto dell'insieme di Cantor, mentre negli altri punti è derivabile ed ha derivata zero. Quindi è una funzione costante in ogni sottointervallo di ${\displaystyle [0,1]}$ che non contenga punti dell'insieme di Cantor (quest'ultimo insieme ha misura nulla), ossia negli intervalli del tipo (0,x₁x₂x₃...x_n022222..., 0,x₁x₂x₃...x_n200000...). Nonostante questo, è crescente (in senso lato).

La funzione di Cantor, ristretta all'insieme di Cantor, è sempre continua, crescente e suriettiva sull'intervallo ${\displaystyle [0,1]}$: questo implica che l'insieme di Cantor non è numerabile. Questa funzione è utile per definire una curva di Peano, cioè una curva che riempie totalmente un quadrato.

• Insieme di Cantor
• Variabile casuale di Cantor
• Curva di Peano
• Curva di Koch

• Wikimedia Commons contiene immagini o altri file su funzione di Cantor

• (EN) Eric W. Weisstein, Funzione di Cantor, su MathWorld, Wolfram Research.

V · D · M Teoria del caos
Teoria delle biforcazioni	Biforcazione a forcone · Biforcazione a nodo sella · Biforcazione imperfetta · Biforcazione transcritica · Biforcazione di Hopf · Larva del pino (sistema dinamico)
Frattali	Arte frattale · Buddhabrot · Burning ship · Compressione frattale · Curva di Koch · Curva di Peano · Curva di Sierpiński · Dimensione di Hausdorff · Dimensione frattale · Funzione di Cantor · Insieme di Cantor · Insieme di Julia · Insieme di Mandelbrot · Frattali per dimensione di Hausdorff · Polvere di Cantor · Sterling · Triangolo di Sierpiński · Dimensione di Minkowski-Bouligand
Attrattori	Attrattore di Lorenz · Attrattore di Hénon · Mappa di Poincaré · Mappa logistica · Mappa a ferro di cavallo · Spazio delle fasi
Teorici del caos	Edward Norton Lorenz · Aleksandr Michajlovič Ljapunov · Benoît Mandelbrot · Edward Ott · Henri Poincaré · David Ruelle · Stephen Wolfram · James Yorke

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica