Emipoliedro
In geometria solida, un emipoliedro è un poliedro stellato uniforme avente alcune delle proprie facce passanti per il proprio centro. Il prefisso "emi" nel nome di questo tipo di poliedri è dovuto al fatto che tali facce tagliano il poliedro in due parti uguali aventi ognuna volume pari a metà del volume del poliedro.[1]
Il prefisso "emi" è talvolta utilizzato per riferirsi al alcuni poliedri proiettivi, come ad esempio l'emicubo, che sono l'immagine di una mappa 2 a 1 di un poliedro sferico con simmetria centrale.
Notazione di Wythoff e figura al vertice
[modifica | modifica wikitesto]Le rappresentazioni di tali poliedri in notazione di Wythoff sono della forma p/(p − q) p/q | r e risultano essere molto simili a quelle dei poliedri cantellati, mentre le loro figure al vertice sono quadrilateri incrociati e la loro incidenza dei vertici è p/q.2r.p/(p − q).2r.[2] Le facce 2r-gonali passano attraverso il centro del poliedro: se rappresentate come facce di un poliedro sferico, esse coprono un intero emisfero e i loro bordi e i loro vertici giacciono su una circonferenza massima.[3]
I nove emipoliedri, di seguito elencati con i propri simboli di Wythoff e incidenza dei vertici, sono:[4]
 Tetraemiesaedro 3/2 3 | 2 (3.4.3/2.4) (p/q = 3, r = 2) |
 Ottaemiottaedro 3/2 3 | 3 (3.6.3/2.6) (p/q = 3, r = 3) |
 Piccolo icosiemidodecaedro 3/2 3 | 5 (3.10.3/2.10) (p/q = 3, r = 5) |
 Grande icosiemidodecaedro 3/2 3 | 5/3 (3.10/3.3/2.10/3) (p/q = 3, r = 5/3) |
 Piccolo dodecaemicosaedro 5/3 5/2 | 3 (5/2.6.5/3.6) (p/q = 5/2, r = 3) |
 Cuboemiottaedro 4/3 4 | 3 (4.6.4/3.6) (p/q = 4, r = 3) |
 Piccolo dodecaemidodecaedro 5/4 5 | 5 (5.10.5/4.10) (p/q = 5, r = 5) |
 Grande dodecaemidodecaedro 5/3 5/2 | 5/3 (5/2.10/3.5/3.10/3) (p/q = 5/2, r = 5/3) |
 Grande dodecaemicosaedro 5/4 5 | 3 (5.6.5/4.6) (p/q = 5, r = 3) |
Si noti che la costruzione caleidoscopica di Wythoff genera gli emipoliedri non orientabili (tutti tranne l'ottaemiottaedro come doppie coperture di una sfera, ossia due emipoliedri coincidenti.
Nel piano euclideo la sequenza di emipoliedri continua con le quattro tassellature stellati riportate di seguito, dove gli apeirogoni appaiono come i summenzionati poligoni equatoriali:
| Tassellatura rettificata originaria |
Diagramma | Solido | Incidenza dei vertici |
Notazione di Wythoff |
Simmetria |
|---|---|---|---|---|---|
 Tassellatura quadrata |
 |
 |
4.∞.4/3.∞ 4.∞.-4.∞ |
∞ | p4m |
 Tassellatura triangolare |
 |
 |
(3.∞.3.∞.3.∞)/2 | 3 ∞ | p6m |
 Tassellatura triesagonale |
 |
 |
6.∞.6/5.∞ 6.∞.-6.∞ |
∞ | |
 |
∞.3.∞.3/2 ∞.3.∞.-3 |
∞ |
Di queste quattro tasellature solo la 6/5 6 | ∞ è generata come una doppia copertura dalla costruzione di Wythoff.
Orientabilità
[modifica | modifica wikitesto]Tra gli emipoliedri, solo l'ottaemiottaedro rappresenta una varietà orientabile.
Duali degli emipoliedri
[modifica | modifica wikitesto]Poiché gli emipoliedri hanno facce passanti per il loro centro, i loro duali hanno vertici posti all'infinito, e più precisamente all'infinito sul piano proiettivo reale.[5] Nella sua opera "Dual Models", Magnus Wenninger rappresenta tali figure come prismi intersecanti, ognuno dei quali si estende all'infinito verso il vertice stesso, così da mantenere la simmetria. Nella comune rappresentazione i prismi costituenti il modello vengono per comodità tagliati a un certo punto della loro altezza. Wenninger ha suggerito di inserire queste nuove figure in una nuova classe di solidi generati per stellazione, chiamati "stellazioni all'infinito". Tuttavia egli ha anche affermato che, strettamente parlando, tali figure non sarebbero in effetti poliedri poiché la loro costruzione non risulta conforme alle comuni definizioni.[5]
Esistono quindi 9 poliedri duali degli emipoliedri, che condividono però solo 5 forme visivamente diverse dato che 8 di loro compongono 4 coppie di poliedri esternamente identici. I membri di tali coppie differiscono tra loro nella disposizione di veri e falsi vertici, laddove per "falso vertice" si intende un punto in cui due spigoli si incrociano e non si uniscono. Tali 5 forme sono:
|
|
|
|
|
| Tetraemiesacrono | Ottaemiottacrono ed esaemiottacrono |
Piccolo icosiemidodecacrono e piccolo dodecaemidodecacrono |
Grande dodecaemidodecacrono e grande icosiemidodecacrono |
Grande dodecaemicosacrono e piccolo dodecaemicosacrono |
| 3 prismi quadrati infiniti intersecanti | 4 prismi esagonali infiniti intersecanti | 6 prismi decagonali infiniti intersecanti | 6 prismi decagrammici infiniti intersecanti | 10 prismi esagonali infiniti intersecanti |
Relazione con i poliedri quasi regolari
[modifica | modifica wikitesto]Gli emipoliedri si presentano in coppie come risultato della facettazione di poliedri quasi regolari con quattro facce incidenti su ogni vertice. Tali poliedri quasi regolari hanno incidenza dei vertici m.n.m.n e i loro spigoli, oltre a formare le facce m- ed n-gonali, vanno poi a formare anche le emi-facce, ossia quelle passanti per il centro, dell'emipoliedro. Gli emipoliedri possono quindi essere ottenuti dai poliedri quasi regolari eliminando gli m-goni o gli n-goni e inserendo quindi le emifacce. Poiché ad essere eliminati possono essere gli m-goni o gli n-goni, allora da ogni poliedro quasi regolare possono essere ottenuti due emipoliedri, ad eccezione dell'ottaedro (o tetratetraedro), dove m = n = 3 e i due tipi di facce sono congruenti.[1] Poiché anche gli emipoliedri, così come i poliedri quasi regolari, hanno due tipi di facce che si alternano attorno a ogni vertice, sono talvolta essi stessi considerati poliedri quasiregolari.[1]
| Poliedro quasiregolare m.n.m.n |
Emi-facce (h-goni) | Emipoliedro con m-goni eliminati n.h.n/n - 1.h |
Emipoliedro con n-goni eliminati m.h.m/m - 1.h |
|---|---|---|---|
 Ottaedro 3.3.3.3 m = 3, n = 3 |
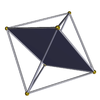 quadrati {4} |
Tetraemiesaedro 3.4.3/2.4 |
Tetraemiesaedro 3.4.3/2.4 |
 Cubottaedro 3.4.3.4 m = 3, n = 4 |
 esagoni {6} |
Cuboemiottaedro 4.6.4/3.6 |
Ottaemiottaedro 3.6.3/2.6 |
 Icosidodecaedro 3.5.3.5 m = 3, n = 5 |
 decagoni {10} |
Piccolo dodecaemidodecaedro 5.10.5/4.10 |
Piccolo icosiemidodecaedro 3.10.3/2.10 |
 Dodecadodecaedro 5.5/2.5.5/2 m = 5, n = 5/2 |
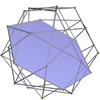 Esagoni {6} |
Piccolo dodecaemicosaedro 5/2.6.5/3.6 |
Grande dodecaemicosaedro 5.6.5/4.6 |
 Grande icosidodecaedro 3.5/2.3.5/2 m = 3, n = 5/2 |
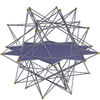 Decagrammi {10/3} |
Grande dodecaemidodecaedro 5/2.10/3.5/3.10/3 |
Grande icosiemidodecaedro 3.10/3.3/2.10/3 |
Qui m ed n corrispondono ai precedenti p/q e h corrisponde al precedente 2r.
Note
[modifica | modifica wikitesto]- ^ a b c George Hart, Quasiregular Polyhedra, su Virtual Polyhedra: The Encyclopedia of Polyhedra, 1996. URL consultato il 20 ottobre 2021.
- ^ Zvi Har’El, Uniform Solution for Uniform Polyhedra, Israel Institute of Technology, 1993, pp. 10. URL consultato il 6 giugno 2021 (archiviato dall'url originale l'8 giugno 2021).
- ^ Harold Scott Macdonald Coxeter, Michael Selwyn Longuet-Higgins e J. C. P. Miller, Uniform Polyhedra, in Philosophical Transactions of The Royal Society, vol. 246, n. 916, The Royal Society Publishing, 1954, pp. 401-50. URL consultato il 6 giugno 2021.
- ^ Magnus Wenninger, Polyhedron Models, Cambridge University Press, 1974, ISBN 978-0-521-09859-5, MR 0467493.
- ^ a b Magnus Wenninger, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 730208.
