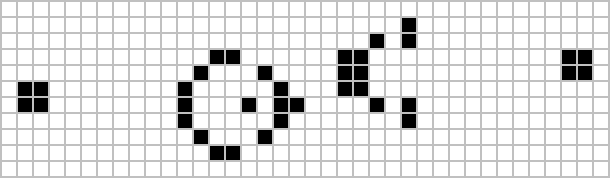
Gioco della vita

Il Gioco della vita (Game of Life in inglese, noto anche solo come Life) è un automa cellulare sviluppato dal matematico inglese John Conway sul finire degli anni sessanta. Il Gioco della vita è l'esempio più famoso di automa cellulare: il suo scopo è quello di mostrare come comportamenti simili alla vita possano emergere da regole semplici e interazioni a molti corpi, principio che è alla base dell'ecobiologia, la quale si rifà anche alla teoria della complessità. Del gioco sono poi state sviluppate versioni con differenti topologie, ad esempio tridimensionali^[1][2], differenti regole biologiche, e differenti tipi di cellule.

Ha fatto la sua prima apparizione in pubblico nell'edizione dell'ottobre 1970 di Scientific American, nella rubrica «Giochi matematici»^[3] di Martin Gardner. Dal punto di vista teorico è interessante perché ha le potenzialità di una macchina di Turing universale: in altre parole, ogni cosa che può essere elaborata algoritmicamente può essere elaborata nel contesto del Game of Life, rendendolo di fatto Turing equivalente.^[4][5]

Dal momento della sua pubblicazione ha ottenuto molto interesse grazie ai modi sorprendenti in cui le diverse configurazioni possono evolvere. Il gioco è un esempio di sviluppo e auto-organizzazione. È interessante per scienziati, matematici e economisti osservare il modo in cui schemi complessi possono emergere dall'implementazione di regole assai semplici.

Il Gioco della vita ha una grande quantità di modelli conosciuti che emergono da particolari configurazioni iniziali. Poco tempo dopo la pubblicazione furono scoperti i modelli dell'R-pentamino e dell'aliante, i quali incrementarono l'interesse verso il gioco. La sua popolarità fu aiutata dal fatto che fu immessa sul mercato una nuova generazione di minicomputer, permettendo così di lasciare il gioco in esecuzione per ore su queste macchine che sarebbero state altrimenti inutilizzate durante la notte. Per molti affezionati, Life era semplicemente una sfida di programmazione, un modo divertente per non sprecare i cicli delle CPU. Per molti altri, invece, Life aveva più connotati filosofici. Divenne oggetto di una sorta di culto amatoriale durante gli anni settanta e nella prima metà degli anni ottanta.

Si tratta in realtà di un gioco senza giocatori, intendendo che la sua evoluzione è determinata dal suo stato iniziale, senza necessità di alcun input da parte di giocatori umani. Si svolge su una griglia di caselle quadrate (celle) che si estende all'infinito in tutte le direzioni; questa griglia è detta mondo. Ogni cella ha 8 vicini, che sono le celle ad essa adiacenti, includendo quelle in senso diagonale. Ogni cella può trovarsi in due stati: viva o morta (o accesa e spenta, on e off). Lo stato della griglia evolve in intervalli di tempo discreti, cioè scanditi in maniera netta. Gli stati di tutte le celle in un dato istante sono usati per calcolare lo stato delle celle all'istante successivo. Tutte le celle del mondo vengono quindi aggiornate simultaneamente nel passaggio da un istante a quello successivo: passa così una generazione.

Le transizioni dipendono unicamente dallo stato delle celle vicine in quella generazione:

• Qualsiasi cella viva con meno di due celle vive adiacenti muore, come per effetto d'isolamento;
• Qualsiasi cella viva con due o tre celle vive adiacenti sopravvive alla generazione successiva;
• Qualsiasi cella viva con più di tre celle vive adiacenti muore, come per effetto di sovrappopolazione;
• Qualsiasi cella morta con esattamente tre celle vive adiacenti diventa una cella viva, come per effetto di riproduzione.

I primi modelli interessanti nel Gioco della Vita sono stati scoperti senza l'uso di computer. I più semplici schemi statici ("still life") e modelli ripetuti ("oscillatori" - superset di morti) sono stati scoperti mentre si monitoravano i destini di varie piccole configurazioni di avvio utilizzando carta grafica, lavagne, tavole fisiche (come Go) e simili. Durante questa prima ricerca, Conway ha scoperto che l'R-pentomino non è riuscito a stabilizzarsi in un piccolo numero di generazioni.

Molti diversi tipi di modelli si verificano nel Gioco della Vita, tra cui le morti, gli oscillatori e gli schemi che si traducono in tutto il board, incluso il velivolo, scoperto da Richard K. Guynel 1970 e diversi tipi di astronavi. Di seguito sono riportati alcuni esempi frequenti di queste tre classi, con le celle vive mostrate in nero e le cellule morte mostrate in bianco.

Il blocco e la barca sono oggetti stabili, il lampeggiatore e il rospo sono oscillatori, l'aliante e l'astronave leggera sono navicelle spaziali che si spostano per il mondo mentre il tempo scorre.

Le configurazioni chiamate methuselah possono evolversi per lungo tempo prima di ripetersi. Il diehard (duro a morire) è uno schema che alla fine scompare, dopo 130 generazioni. L'eptomino di Alessandro Goretti e l'eptomino-P impiegano rispettivamente 172 e 173 generazioni prima di stabilizzarsi in una forma statico-oscillatoria. La ghianda impiega 5206 generazioni per generare 13 alianti e poi si stabilizza nella forma di tanti oscillatori.

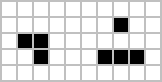
La configurazione dei due eptomini è: 3x3 (111101101); 5x2 (0111011011)

Diehard	Ghianda

Nell'apparizione originale del gioco, Conway offrì un premio in denaro per un qualunque schema che crescesse indefinitamente. Il primo fu trovato da Bill Gosper nel novembre del 1970. Questi schemi includono i gun (fucili), che sono stazionari e sparano alianti o altre navicelle, i fumatori, che si muovono lasciando dietro di loro una coda di detriti statici, e i rastrelli, che si muovono ed emettono navicelle. Gosper ha più tardi scoperto uno schema con un tasso di crescita quadratico, chiamato reattore, che lavorava lasciando dietro di sé una coda di fucili. Da allora sono state create complicate costruzioni, tra cui porte logiche per alianti, un sommatore, un generatore di numeri primi, e una cella che emula lo stesso Gioco della vita riscalato nello spazio e nel tempo.

Il primo emettitore di alianti scoperto è tuttora il più piccolo conosciuto:

Schemi più semplici, anch'essi dotati di crescita infinita, furono scoperti più tardi. Tutti e tre i seguenti schemi hanno una crescita infinita. I primi due creano un motore di interruttori a blocchi (blocklaying switch engine) ciascuno, mentre il terzo ne crea due. Il primo ha solo 10 celle vive (che sono state dimostrate essere il minimo). Il secondo si situa in un quadrato 5 per 5. Il terzo (di Paul Callahan) è alto solo una riga.

Sono possibili interazioni interessanti tra alianti e altri oggetti. Per esempio, se due alianti colpiscono un blocco nella maniera giusta, il blocco si muove verso la sorgente degli alianti. Se tre alianti sono lanciati nella giusta maniera il blocco si muove allontanandosi dalla sorgente degli alianti. Questa memoria a blocchi può essere usata per simulare un contatore. È possibile costruire porte logiche AND, OR e NOT usando alianti. È possibile costruire una configurazione che agisca come una macchina a stati finiti connessa a due contatori.^[6] Questo ha lo stesso potere computazionale di una macchina di Turing universale, così il Gioco della vita è potente quanto un qualunque computer con memoria infinita: è Turing equivalente. Inoltre, uno schema può contenere un insieme di fucili che si combinano per creare nuovi oggetti, tra cui copie dello schema originale. Può essere costruito un costruttore universale che contenga un computer Turing equivalente, e che può costruire numerosi tipi di oggetti complessi, includendo copie di se stesso.^[7]

• Nel videogioco Factorio è possibile riprodurre il Gioco della vita.^[8][9][10]
• Nel videogioco sandbox The Powder Toy è possibile posizionare delle particelle denominate gioco della vita.
• Nel gioco per cellulare Theotown è possibile creare del terreno con il Gioco della vita.^[11]
• Nel videogioco sandbox Worldbox esistono due poteri ispirati proprio al Gioco della vita
• Life: the Social Game (social game ispirato al Gioco della vita di John Conway) - sito ufficiale

• Martin Gardner, The fantastic combinations of John Conway's new solitaire game "Life", Scientific American, 223, ottobre 1970, pp. 120–123
• (EN) Martin Gardner, The Game of Life, in Wheels, Life, and Other Mathematical Amusements, 1983, pp. 214-257, ISBN 0-7167-1589-9.
• Life (1) (JPG), in MCmicrocomputer, n. 37, Roma, Technimedia, gennaio 1985, p. 26, ISSN 1123-2714 (WC · ACNP).
• Life (2) (JPG), in MCmicrocomputer, n. 38, Roma, Technimedia, febbraio 1985, p. 34, ISSN 1123-2714 (WC · ACNP).
• Life (3) (JPG), in MCmicrocomputer, n. 39, Roma, Technimedia, marzo 1985, p. 36, ISSN 1123-2714 (WC · ACNP).
• Life (4) (JPG), in MCmicrocomputer, n. 40, Roma, Technimedia, aprile 1985, p. 36, ISSN 1123-2714 (WC · ACNP).

• Formica di Langton
• Navicella (automa cellulare)
• Oscillatore (automa cellulare)
• Quasicristallo
• Roger Penrose

• Wikibooks contiene un'implementazione in C++ del Gioco della vita
• Wikimedia Commons contiene immagini o altri file su Gioco della vita

• (EN) Game of Life, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Gioco della vita, su MathWorld, Wolfram Research.
• (EN) Life Lexicon, su argentum.freeserve.co.uk. URL consultato il 9 luglio 2010 (archiviato dall'url originale il 26 maggio 2013).
• (EN) Golly, su golly.sourceforge.net.
• (EN) Conway's Game of Life - A community of Conway's Game of Life and related cellular automata, su conwaylife.com.
• (EN) LifeWiki, su conwaylife.com.
• (EN) Paul Callahan, What is the Game of Life?, su math.com.
• (EN) The fantastic combinations of John Conway's new solitaire game "life", su scientificamerican.com.

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica