La formica di Langton è un automa a stati finiti bidimensionale con un insieme di regole molto semplice ma in grado di creare figure molto complicate. È stato inventato nel 1986 da Chris Langton.

Le celle di una griglia sono colorate ognuna di bianco o nero. La "formica" sta su uno di essi.

La formica può spostarsi in ognuna delle 4 direzioni cardinali, seguendo le seguenti regole:

• su una cella nera, gira a destra di 90°, scambia il colore della cella, si sposta avanti di una cella
• su una cella bianca, gira a sinistra di 90°, scambia il colore della cella, si sposta avanti di una cella

Queste due semplici regole portano ad un comportamento sorprendentemente complesso: se avviate su una griglia completamente bianca, dopo un periodo di apparente caos la formica comincia a costruire un motivo ricorrente di 104 passi che si ripete all'infinito. Altre configurazioni iniziali sembrano convergere a simili schemi ripetitivi, suggerendo che questa cosiddetta "autostrada" sia un attrattore della formica di Langton; tuttavia, nessuno è riuscito a dimostrare che ciò valga per ogni configurazione iniziale.

È stato invece dimostrato che la formica di Langton è Turing-equivalente.

Questo automa può anche essere visto come un automa cellulare, in cui ai colori bianco e nero che riempiono la griglia vengono aggiunti altri 8 colori per la cella dove si trova la formica; essi codificano il colore di quella cella e la direzione della formica (e sono gli unici che danno origine a comportamenti dinamici).

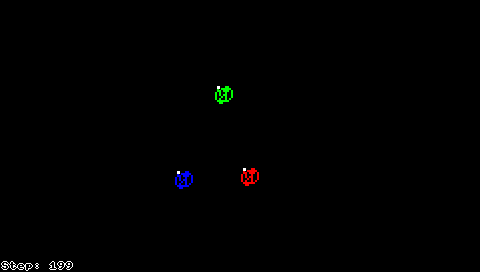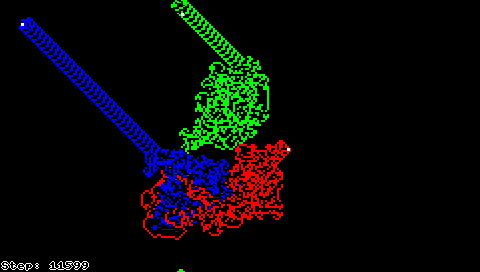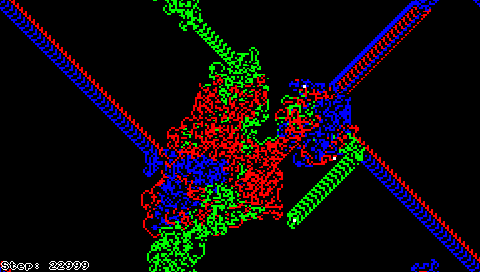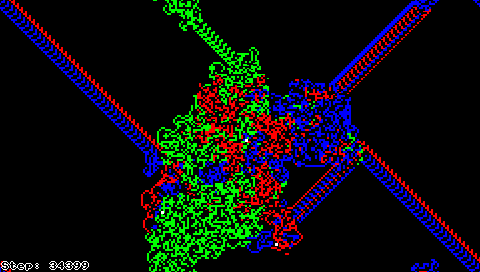
Un'estensione semplice del concetto di formica di Langton è quella in cui vengono utilizzati più di due colori, che la formica cambia in modo ciclico. Per indicare schematicamente estensioni di questo tipo, è sufficiente specificare, per ognuno dei colori, una lettera che indichi quale direzione la formica prenda in corrispondenza: D o S. Secondo questo schema, la formica di Langton "classica" segue la regola SD.

Alcune di queste formiche di Langton "estese" producono configurazioni che si ripetono sempre simmetricamente. Uno dei più semplici esempi è dato dalla formica DSSD. Una condizione sufficiente perché ciò accada è che la regola della formica, sia composta da coppie consecutive di lettere uguali (eventualmente dopo avere spostato l'ultima lettera all'inizio).

Nel 2000, Gajardo ed altri sono riusciti a descrivere una configurazione che calcola il valore di un qualsiasi circuito booleano sfruttando la traiettoria di una singola formica di Langton.^[1] Ciò implica che è possibile simulare una macchina di Turing utilizzando la traiettoria della formica come computazione, ovvero che la formica di Langton, vista come meccanismo di calcolo formale, è turing-equivalente.

2.nell'aggiornamento 20w 14infinito di Minecraft viene inserito un blocco chiamato la formica di Langton che la simula perfettamente.

• Automa a stati finiti
• Gioco della vita

• Wikimedia Commons contiene immagini o altri file su Formica di Langton

• (EN) Further Travels with my Ant, di D. Gale, J. Propp, S. Sutherland, and S. Troubetzkoy: un articolo (in formato PostScript o TeX) contenente una prova delle suddette condizioni sufficienti per la simmetricità di una configurazione.
• Implementazione in Python della formica di Langton^{[collegamento interrotto]}, con diverse regole disponibili.
• (EN) Implementazione in C della formica di Langton, con la possibilità di inserire più formiche.
• (EN) Estensioni della formica di langton, con alcune implementazioni.
• (EN) Implementazione in Java con colori multipli e formiche programmabili.
• (EN) Implementazione per Windows Archiviato il 28 agosto 2010 in Internet Archive., con la possibilità di aggiungere varie formiche oltre che ostacoli.
• (EN) Un editoriale divulgativo di Scientific American Mathematical che parte dalla formica di Langton's come una metafora di una Teoria del tutto.
• (EN) Implementazione in Java, con varie griglie e grafi modificabili; mostra come la formica può emulare porte logiche.
• (EN) Vermi di Paterson, su maa.org. URL consultato il 1º maggio 2019 (archiviato dall'url originale il 3 giugno 2013).
• (IT, EN) Animazione esplicativa, su youtube.com.