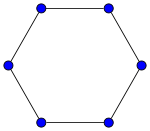
Nella teoria dei grafi, un grafo ciclo o grafo circolare è un grafo che consiste di un unico ciclo o, in altre parole, di un certo numero di vertici connessi in una catena chiusa. Il grafo ciclo con n vertici è chiamato C_n. Il numero di vertici in C_n uguaglia il numero di spigoli, e ogni vertice ha grado 2; ossia, ogni vertice ha esattamente due spigoli incidenti con esso.

Esistono molti sinonimi di "grafo ciclo". Questi comprendono grafo ciclo semplice e grafo ciclico, sebbene il secondo termine sia usato meno spesso, perché può riferirsi a grafi che semplicemente non sono aciclici. Tra i teorici dei grafi, si usano spesso anche ciclo, poligono o n-gono. Un ciclo con un numero pari di vertici è chiamato ciclo pari; un ciclo con un numero dispari di vertici è chiamato ciclo dispari.

Un grafo ciclo è:

• Connesso
• 2-regolare
• Euleriano
• Hamiltoniano
• 2-colorabile sui vertici, se e solo se ha un numero pari di vertici. Più generalmente, un grafo è bipartito se e solo se ha un numero dispari di cicli (Kőnig, 1936)
• 2-colorabile sugli spigoli, se e solo se ha un numero pari di vertici
• 3-colorabile sui vertici e 3-colorabile sugli spigoli, per qualsiasi numero di vertici
• Un grafo a distanza unitaria

In aggiunta:

• Poiché i grafi ciclo possono essere disegnati come poligoni regolari, le simmetrie di un n-ciclo sono le stesse di un poligono regolare con n lati, il gruppo diedrico di ordine 2n. In particolare, esistono simmetrie che portano qualsiasi vertice a qualsiasi altro vertice, e qualsiasi spigolo a qualsiasi altro spigolo, perciò l'n-ciclo è un grafo simmetrico.

Un grafo ciclo diretto è una versione diretta di un grafo ciclo, con tutti gli spigoli orientati nella stessa direzione.

In un grafo diretto, un insieme di spigoli che contiene almeno uno spigolo (o arco) di ciascun ciclo diretto è chiamato insieme di archi in retroazione. Similmente, un insieme di vertici contenente almeno un vertice di ciascun ciclo diretto è chiamato insieme di vertici in retroazione.

Un grafo ciclo diretto ha grado in entrata uniforme 1 e grado in uscita uniforme 1.

I grafi ciclo diretti sono grafi di Cayley per i gruppi ciclici (vedi ad es. Trevisan).

• Cammino (teoria dei grafi)
• Grafo bipartito completo
• Grafo completo
• Grafo nullo

• Wikimedia Commons contiene immagini o altri file su grafo ciclo

• (EN) Eric W. Weisstein, Grafo ciclo, su MathWorld, Wolfram Research.
• (EN) Luca Trevisan, Characters and Expansion.

Portale Matematica: accedi alle voci di Teknopedia che trattano di Matematica