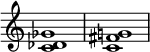Tricordo viennese

Da Teknopedia, l'enciclopedia libera.
Vai alla navigazione Vai alla ricerca

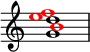
Nella teoria musicale, un Tricordo viennese (anche chiamato accordo di quarta viennese e accordo tritono di quarta[1]), così chiamato dalla Seconda scuola di Vienna, è un insieme con forma primaria (0,1,6). Il suo numero di Forte è 3-5. Gli insiemi Do–Re♭–Sol♭ e Do–Fa♯–Sol sono entrambi esempi di tricordi viennesi, sebbene possano essere arrangiati in molti modi.[2]

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 4/4 <c des ges>1 <c fis g!> } }

Secondo Henry Martin, "compositori come Webern... sono parziali con i tricordi 016, dato il loro inserimento "più dissonante" degli intervalli di classe 1 e 6."[3]

Nel jazz e nella musica popolare l'accordo di solito ha una funzione dominante, essendo il terzo, il settimo e sesto/tredicesimo aggiunto di un accordo dominante con radice[4] elisa (e quinto, come nell'accordo del jazz).

{ \override Score.TimeSignature #'stencil = ##f \new Staff << \new Voice \relative c'' { \clef treble \time 4/4 \voiceOne <g d'>1 } \new Voice \relative c'' { \clef treble \time 4/4 \voiceOne \override NoteHead.color = #red b1 } \new Voice \relative c'' { \clef treble \time 4/4 \voiceTwo \override NoteHead.color = #red <e f>1 } >> }

Note

[modifica | modifica wikitesto]
  1. ^ DeLone, et al (1975). Aspects of 20th Century Music, p. 348. ISBN 0-13-049346-5.
  2. ^ Paddison, Max and Deliège, Irène (2010). Contemporary Music: Theoretical and Philosophical Perspectives, p. 62. ISBN 9781409404163.
  3. ^ Martin, Henry (Winter, 2000). "Seven Steps to Heaven: A Species Approach to Twentieth-Century Analysis and Composition", p. 149, Perspectives of New Music, Vol. 38, No. 1, pp. 129-168.
  4. ^ Forte, Allen (2000). "Harmonic Relations: American Popular Harmonies (1925-1950) and Their European Kin", pp. 5-36, Traditions, Institutions, and American Popular Music (Contemporary Music Review, Vol. 19, Part 1), p. 7. Routledge. Covach, John and Everett, Walter; eds. ISBN 90-5755-120-9.

Collegamenti esterni

[modifica | modifica wikitesto]
  Portale Musica classica: accedi alle voci di Teknopedia che trattano di musica classica
Estratto da "https://it.wikipedia.org/w/index.php?title=Tricordo_viennese&oldid=131903345"