Indice
PGF/TikZ
| PGF/TikZ software | |
|---|---|
 | |
| Genere | Computer grafica |
| Sviluppatore | Till Tantau, Christian Feuersänger |
| Ultima versione | 3.1.10 (15 gennaio 2023) |
| Sistema operativo | Multipiattaforma |
| Licenza | GNU General Public Licence e LPPL (licenza libera) |
| Sito web | github.com/pgf-tikz/pgf |
PGF/TikZ è una coppia di linguaggi di programmazione per la produzione di grafica vettoriale (ad esempio illustrazioni e disegni tecnici) a partire da una descrizione geometrica/algebrica, con funzionalità standard tra cui il disegno di punti, linee, frecce, percorsi, cerchi, ellissi e poligoni. PGF è un linguaggio di basso livello, mentre TikZ è un insieme di macro di livello superiore che utilizzano PGF. I comandi PGF e TikZ di alto livello vengono richiamati come macro TeX, ma a differenza di PSTricks, la grafica PGF/TikZ è descritta in un linguaggio che ricorda MetaPost. Till Tantau è l'ideatore dei linguaggi PGF e TikZ. È anche lo sviluppatore principale dell'unico interprete noto per PGF e TikZ, scritto in TeX. PGF è l'acronimo di "Portable Graphics Format". TikZ è stato introdotto nella versione 0.95 di PGF ed è un acronimo ricorsivo di "TikZ ist kein Zeichenprogramm" (in tedesco "TikZ non è un programma di disegno").
Introduzione
[modifica | modifica wikitesto]L'interprete PGF/TikZ può essere utilizzato dai popolari pacchetti macro LaTeX e ConTeXt, e anche direttamente da TeX.[1] Poiché TeX stesso non si occupa di grafica, l'interprete supporta diverse backend di output TeX: dvips, dvipdfm/dvipdfmx/xdvipdfmx, TeX4ht e il driver di output PDF interno di pdftex.[1] A differenza di PSTricks, PGF può quindi produrre direttamente un output PostScript o PDF, ma non può utilizzare alcune delle funzionalità di programmazione PostScript più avanzate che PSTricks può utilizzare a causa dell'effetto "minimo comune denominatore".[2] PGF/TikZ è dotato di un'estesa documentazione; la versione 3.1.4a del manuale ha oltre 1300 pagine.[1]
L'ambiente picture di LaTeX può anche essere utilizzato come front-end per PGF utilizzando il pacchetto pgfpict2e.[1]
Il progetto è in costante sviluppo a partire dal 2005.[3] La maggior parte dello sviluppo fino al 2018 è stato svolto da Till Tantau e, da allora, Henri Menke è stato il principale collaboratore.[4] La versione 3.0.0 è stata rilasciata il 20 dicembre 2013.[5] Una delle principali novità di questa versione è la possibilità di disegnare grafici utilizzando il pacchetto graphdrawing, il quale richiede LuaTeX.[6] Questa versione ha anche aggiunto un nuovo metodo di visualizzazione dei dati e il supporto per l'output SVG diretto tramite il nuovo driver dvisvgm.[5]
Esportare
[modifica | modifica wikitesto]Diversi editor grafici possono produrre output per PGF/TikZ, come il programma KDE Cirkuit[7] e il programma di disegno matematico GeoGebra.[8] L'esportazione in TikZ è disponibile anche come estensione per Inkscape,[9] Blender,[10] MATLAB,[11] matplotlib,[12] Gnuplot,[13] Julia,[14] e R.[15] Il pacchetto circuit-macros[16] di m4 macros esporta schemi di circuito elettrico in TikZ utilizzando il comando dpic -g.[17] Il programma dot2tex può convertire i file nel linguaggio di descrizione del grafico DOT in PGF/TikZ.[18]
Librerie
[modifica | modifica wikitesto]TikZ contiene librerie per disegnare facilmente molti tipi di diagrammi, come le seguenti (in ordine alfabetico in base al nome della libreria):[1]
- Computer grafica 3D –
3d - Automa a stati finiti e Macchina di Turing –
automata - Sistema di coordinate –
calc - Calendario –
calendar - Catene: nodi generalmente connessi da lati e disposti in righe e colonne –
chain - Circuito logico e schema elettrico –
circuits.logicecircuits.ee - Modello E-R –
er - Diagrammi di sviluppo piano di un poliedro –
folding - Raffigurazione di un grafo con opzione di allineamento automatico –
graphdrawing - Sistema di Lindenmayer –
lindenmayersystems - Sequenze matematiche operazione aritmetica –
math - Matrice –
matrix - Mappa mentale –
mindmap - Disegni in prospettiva –
perspective - Rete di Petri –
petri - Circuito quantico –
quantikz - RDF annotazioni semantiche (solamente in output SVG) –
rdf - Forme e simboli speciali –
shapes.geometricandshapes.symbols - Ingrandimento di una parte di un inserto –
spy - Grafica vettoriale in SVG –
svg.path - Diagrammi ad albero –
trees - Turtle graphics –
turtle - Zoom e Panning –
views
Galleria
[modifica | modifica wikitesto]Le immagini seguenti sono state create con TikZ e mostrano alcuni esempi delle tipologie grafiche che possono essere prodotte. Il collegamento in ogni didascalia rimanda al codice sorgente dell'immagine.
-
Tavola periodica degli elementi chimici(librerie utilizzate:
cac, shapes) -
Elica radicata(libreria utilizzata: calc)
-
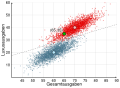
Grafico di due variabili distribuite normalmente con grande varianza(librerie utilizzate:
arrows,positioning) -
Rendering di ipersuperficie (librerie utilizzate:
arrows,calc,decorations.markings,intersections,positioning) -
Modello di miscela gaussiana bayesiana (librerie utilizzate:
arrows,backgrounds,calc,fit,matrix,patterns,plotmarks,shadows) -
Circuiti equivalenti dei condensatori(libreria utilizzata: arrows)
-
Diagramma che mostra diversi tipi di test sulla media (librerie utilizzate:
arrows,shapes) -
Grafico a gradiente di una funzione (libreria utilizzata: arrows
.meta) -
Scudo della Trinità con le quattro relazioni (librerie utilizzate:
graphdrawing,graphs,quotes) -
Grafico delle unità di lunghezza inglesi
-
Omomorfismo grafico in C5 (libreria utilizzata: calc)
-
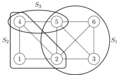
Sottografi della partizione di Krausz di un dato grafico lineare
-
Elenco di adiacenza di un grafico implementato come array di elenchi concatenati (librerie utilizzate:
arrows,calc,positioning,shapes.multipart)
Note
[modifica | modifica wikitesto]- ^ a b c d e CTAN.org, https://mirrors.ctan.org/graphics/pgf/base/doc/pgfmanual.pdf. URL consultato il 17 giugno 2019.
- ^ Till Tantau, Copia archiviata (PDF), su CTAN.org. URL consultato il 6 May 2010 (archiviato dall'url originale il 9 gennaio 2011).
- ^ GitHub.com, https://github.com/pgf-tikz/pgf/commits/master. URL consultato il 17 giugno 2019.
- ^ GitHub.com, https://github.com/pgf-tikz/pgf/graphs/contributors. URL consultato il 17 giugno 2019.
- ^ a b SourceForge.net, https://sourceforge.net/projects/pgf/files/pgf/version%203.0.0. URL consultato il 17 giugno 2019.
- ^ vol. 17, DOI:10.7155/jgaa.00301, https://oadoi.org/10.7155/jgaa.00301.
- ^ Copia archiviata, su uni-klu.ac.at. URL consultato il 17 giugno 2019 (archiviato dall'url originale il 14 giugno 2019).
- ^ wiki.geogebra.org, https://wiki.geogebra.org/en/Export_to_LaTeX_(PGF,_PSTricks)_and_Asymptote. URL consultato il 17 giugno 2019.
- ^ GitHub.com, https://github.com/kjellmf/svg2tikz. URL consultato il 17 giugno 2019.
- ^ GitHub.com, https://github.com/kjellmf/blend2tikz. URL consultato il 17 giugno 2019.
- ^ MathWorks.com, https://www.mathworks.com/matlabcentral/fileexchange/22022-matlab2tikz-matlab2tikz. URL consultato il 17 giugno 2019.
- ^ GitHub.com, https://github.com/nschloe/tikzplotlib. URL consultato il 17 giugno 2019.
- ^ gnuplot.info, http://www.gnuplot.info/docs_5.2/Gnuplot_5.2.pdf. URL consultato il 17 giugno 2019.
- ^ docs.juliaplots.org, https://docs.juliaplots.org/latest/backends/. URL consultato il 27 febbraio 2024.
- ^ cran.r-project.org, https://cran.r-project.org/package=tikzDevice. URL consultato il 17 giugno 2019.
- ^ CTAN.org, https://ctan.org/pkg/circuit-macros/. URL consultato il 15 April 2020.
- ^ Copia archiviata, su ece.uwaterloo.ca. URL consultato il 15 April 2020 (archiviato dall'url originale il 19 aprile 2012).
- ^ dot2tex.readthedocs.io, https://dot2tex.readthedocs.io/.
Bibliografia
[modifica | modifica wikitesto]- n. 1, ISSN 1556-6994, https://www.tug.org/pracjourn/2007-1/mertz/. Conference talk video (Archiviato da archive.org) basasto su una versione precedente del testo.
- n. 1, ISSN 1556-6994, https://www.tug.org/pracjourn/2007-1/beccari/. Comparison of several graphics systems in LaTeX.
- Marc van Dongen, LaTeX and Friends, X.media.publishing book series, Springer-Verlag, 2012, DOI:10.1007/978-3-642-23816-1, ISBN 978-3-642-23815-4, OCLC 746835167. Secondo a 2011 review of the book in TUGboat: "It contains a detailed introduction to the TikZ suite—probably one of the best existing descriptions of this highly useful package."
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su PGF/TikZ
Wikimedia Commons contiene immagini o altri file su PGF/TikZ