Notazione di Voigt

In algebra multilineare la notazione di Voigt, nota anche come notazione di Mandel-Voigt, notazione di Nye o notazione di Kelvin, è un modo di rappresentare i tensori simmetrici riducendone l'ordine. L'idea di base sta nel rappresentare il tensore unicamente con le sue componenti indipendenti.

Ad esempio, la matrice simmetrica ${\displaystyle {\underline {\underline {X}}}}$può essere rappresentata da un vettore ${\displaystyle {\underline {x}}}$ nel seguente modo:

${\displaystyle {\underline {\underline {X}}}={\begin{bmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{bmatrix}}\implies {\underline {x}}=\{x_{11},\ x_{22},\ x_{12}\}}$

Una semplice regola mnemonica per la scrittura di un tensore simmetrico secondo la notazione di Voigt, può essere la seguente:

Presa ad esempio una matrice 3×3, che è un tensore di ordine 2, si prenda la matrice triangolare superiore associata, le componenti del vettore corrispondente saranno nell'ordine:

1. I termini lungo la diagonale
2. I termini incontrati risalendo la terza colonna
3. I termini sulla prima riga, partendo dal fondo, sino a ricongiungersi con la diagonale

${\displaystyle \implies {\underline {\sigma }}=\{\sigma _{xx},\ \sigma _{yy},\ \sigma _{zz},\ \sigma _{yz},\ \sigma _{xz},\ \sigma _{xy}\}}$

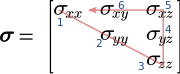
In alternativa si può prendere la matrice triangolare inferiore e chiudere il triangolo in senso opposto.

${\displaystyle {\begin{bmatrix}\sigma _{xx}&&\\\sigma _{yx}&\sigma _{yy}&\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{bmatrix}}\implies {\underline {\sigma }}=\{\sigma _{xx},\ \sigma _{yy},\ \sigma _{zz},\ \sigma _{zy},\ \sigma _{zx},\ \sigma _{yx}\}}$

Le applicazioni di questa notazione sono molteplici. Casi notevoli sono il metodo degli elementi finiti e la legge di Hooke generalizzata.

Prendendo ad esempio quest'ultima si ha:

${\displaystyle \sigma _{ij}=C_{ijkl}\varepsilon _{kl}}$

dove ${\displaystyle \sigma }$ è il tensore degli sforzi, ${\displaystyle \varepsilon }$ il tensore delle deformazioni, tensori di ordine 2 rappresentabili come matrici, e ${\displaystyle C}$ è una matrice 6×6 detta matrice di rigidezza costitutiva:

${\displaystyle {\underline {\underline {\sigma }}}={\begin{bmatrix}\sigma _{xx}&\tau _{yx}&\tau _{zx}\\\tau _{xy}&\sigma _{yy}&\tau _{zy}\\\tau _{xz}&\tau _{yz}&\sigma _{zz}\end{bmatrix}}\qquad {\underline {\underline {\varepsilon }}}={\begin{bmatrix}\varepsilon _{xx}&\gamma _{yx}/2&\gamma _{zx}/2\\\gamma _{xy}/2&\varepsilon _{yy}&\gamma _{zy}/2\\\gamma _{xz}/2&\gamma _{yz}/2&\varepsilon _{zz}\end{bmatrix}}}$

Riscrivendo la legge di Hooke riscritta con la notazione di Voigt si ha:

${\displaystyle \sigma _{i}=C_{ij}\varepsilon _{j}}$

dove ${\displaystyle \sigma }$ è il vettore delle tensioni, ${\displaystyle \varepsilon }$ il vettore delle deformazioni e ${\displaystyle C}$ la matrice di rigidezza costitutiva:

${\displaystyle {\underline {\sigma }}={\begin{Bmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\tau _{xy}\\\tau _{zx}\\\tau _{yz}\end{Bmatrix}}\qquad {\underline {\varepsilon }}={\begin{Bmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\gamma _{xy}\\\gamma _{zx}\\\gamma _{yz}\end{Bmatrix}}}$

• Wikimedia Commons contiene immagini o altri file su Notazione di Voigt

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica