Formula di differenziazione all'indietro

La formula di differenziazione all'indietro (BDF, dall'inglese backward differentiation formula) è una famiglia di metodi impliciti per l'integrazione numerica di equazioni differenziali ordinarie. Sono metodi lineari multipasso che, dati una funzione e un istante temporale, forniscono un valore approssimato della derivata della funzione utilizzando i risultati dei calcoli per istanti temporali precedenti e aumentando così l'accuratezza dell'approssimazione. Questi metodi sono usati specialmente per la soluzione di equazioni differenziali rigide.

Le BDF sono usate per risolvere il seguente problema ai valori iniziali:

${\displaystyle y'=f(y,t),\quad y(t_{0})=y_{0}}$

Una generica BDF può essere scritta come:

${\displaystyle \sum _{k=0}^{s}a_{k}y_{n+k}=h\beta f(y_{n+s},t_{n+s})}$

dove ${\displaystyle h}$ indica il passo di integrazione e ${\displaystyle t_{n}=t_{0}+nh}$. I coefficienti ${\displaystyle a_{k}}$ e ${\displaystyle \beta }$ sono scelti in modo tale che il metodo raggiunga l'ordine ${\displaystyle s}$, che è il massimo possibile.

I metodi BDF sono impliciti, perciò richiedono la risoluzione di equazioni non lineari ad ogni passo di integrazione. Di solito, per questo scopo si usa un metodo di Newton modificato.

Le BDF per s da 1 a 6 sono:

• BDF1: ${\displaystyle y_{n+1}-y_{n}=hf(y_{n+1},t_{n+1})}$ (che equivale al metodo di Eulero all'indietro);
• BDF2: ${\displaystyle y_{n+2}-{\frac {4}{3}}y_{n+1}+{\frac {1}{3}}y_{n}={\frac {2}{3}}hf(y_{n+2},t_{n+2})}$;
• BDF3: ${\displaystyle y_{n+3}-{\frac {18}{11}}y_{n+2}+{\frac {9}{11}}y_{n+1}-{\frac {2}{11}}y_{n}={\frac {6}{11}}hf(y_{n+3},t_{n+3})}$;
• BDF4: ${\displaystyle y_{n+4}-{\frac {48}{25}}y_{n+3}+{\frac {36}{25}}y_{n+2}-{\frac {16}{25}}y_{n+1}+{\frac {3}{25}}y_{n}={\frac {12}{25}}hf(y_{n+4},t_{n+4})}$;
• BDF5: ${\displaystyle y_{n+5}-{\frac {300}{137}}y_{n+4}+{\frac {300}{137}}y_{n+3}-{\frac {200}{137}}y_{n+2}+{\frac {75}{137}}y_{n+1}-{\frac {12}{137}}y_{n}={\frac {60}{137}}hf(y_{n+5},t_{n+5})}$;
• BDF6: ${\displaystyle y_{n+6}-{\frac {360}{147}}y_{n+5}+{\frac {450}{147}}y_{n+4}-{\frac {400}{147}}y_{n+3}+{\frac {225}{147}}y_{n+2}-{\frac {72}{147}}y_{n+1}+{\frac {10}{147}}y_{n}={\frac {60}{147}}hf(y_{n+6},t_{n+6})}$.

Metodi con s ≥ 7 non sono utilizzati perché non sono zero-stabili.

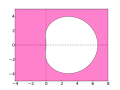
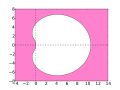
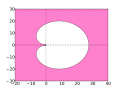
La regione di stabilità del metodo BDF1 comprende l'intera parte sinistra del piano complesso, quindi questo metodo è A-stabile e può essere utilizzato per la risoluzione di equazioni rigide. Le regioni di stabilità delle BDF di ordine superiore invece contengono la quasi totalità del semipiano sinistro, inclusa la parte negativa dell'asse reale.

• La regione di stabilità di ciascuna BDF nel piano complesso è colorata in rosa.
• 
  BDF1
• 
  BDF2
• 
  BDF3
• 
  BDF4
• 
  BDF5
• 
  BDF6

• (EN) Endre Süli e David F. Mayers, An Introduction to Numerical Analysis, Cambridge, Cambridge University Press, 2003, ISBN 0521810264.

• Equazione differenziale ordinaria
• Metodi di soluzione numerica per equazioni differenziali ordinarie

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica