| SAGE software | |
|---|---|
 | |
| Genere | Sistema di algebra computazionale Analisi numerica |
| Sviluppatore | Vari |
| Data prima versione | 2005 |
| Ultima versione | 8.9 (29 settembre 2019) |
| Ultima beta | 9.0.beta5 (11 novembre 2019) |
| Sistema operativo | Linux macOS Microsoft Windows |
| Linguaggio | Fortran Python C++ C Cython |
| Licenza | GPL/Varie: dipendente dai software allegati (licenza libera) |
| Sito web | www.sagemath.org/ |
SageMath (precedentemente noto come Sage o SAGE) è un programma matematico multipiattaforma adatto a risolvere problemi in diverse aree della matematica come algebra, analisi matematica, analisi numerica, calcolo combinatorio, geometria e teoria dei numeri.
La prima versione è stata pubblicata il 24 febbraio del 2005 come software libero con la licenza GNU General Public License. È nato come alternativa open source a Magma, Maple, Mathematica e MATLAB. Il primo sviluppatore del progetto SageMath, William Stein, è un matematico presso l'Università di Washington.
SageMath utilizza il linguaggio di programmazione Python e ne supporta diversi paradigmi di programmazione procedurale, programmazione funzionale e programmazione orientata agli oggetti.
SageMath è disponibile per la piattaforma Linux e Mac OS X (10.4 o superiore); è disponibile anche per Microsoft Windows, in una versione implementata per Oracle VirtualBox.
Funzionalità
[modifica | modifica wikitesto]
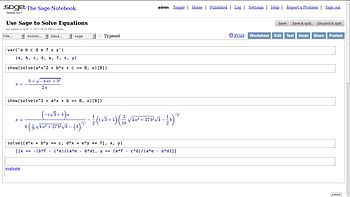
Alcune delle caratteristiche maggiori di SageMath sono:[1].
- L'interfaccia notebook document, per revisionare e riusare precedenti dati in ingresso o in uscita, includendo grafici o caselle di testo usabili per molti web browser incluso Firefox, Opera, Konqueror, e Safari.
Una connessione sicura con HTTPS verso l'interfaccia web notebook è supportata quando sicurezza e riservatezza sono importanti, e consente a Sage di essere utilizzato sia in locale che in remoto. - Una interfaccia testuale a riga di comando usando IPython.
- Il linguaggio di programmazione Python supporta linguaggi procedurali, Funzioni e costrutti riferiti alla Programmazione orientata agli oggetti.
- Supporto per parallel processing usando sia computer con processori Multi core disponibili in molti computer moderni, in aggiunta a sistemi di computer distribuiti (distributed computing).
- Analisi con Maxima e SymPy.
- Algebra lineare con le librerie software GSL, SciPy e NumPy.
- Librerie di Funzioni elementari e funzioni matematiche speciali.
- Grafici 2D e 3D graphs sia per funzioni che per dati.
- Matrice e strumenti di manipolazione dei dati incluso supporto per Array.
- Librerie statistiche varie, utilizzando le funzionalità di R e SciPy.
- Un toolkit per aggiungere interfacce utente per calcoli e applicazioni.[2]
- Strumenti per editor di immagini usando Pylab nonché il linguaggio di programmazione Python.
- Strumenti per visualizzazione ed analisi dei grafi.
- Librerie di funzioni di teoria dei numeri.
- Importazione ed esportazione filtri per dati, immagini, video, suoni, CAD, GIS, documenti e formats biomedicali.
- Supporto per numeri complessi, precisione aritmetica arbitraria e simbolica per funzioni quando ciò è indicato.
- Elaboratore di testo tecnico includente editor di formule la capacità di incorporare all'interno di SageMath documenti di LaTeX.[3]
- Strumenti di rete per connessione a SQL, Java, .NET, C++, FORTRAN fornito da Twisted, questo supporta un gran numero di protocolli tra cu HTTP, NNTP, IMAP, SSH, IRC, FTP e altri.
- Interfacce di alcuni software di terze parti come Mathematica, Magma, e Maple, che permette agli utenti di assemblare software e confrontare risultati e prestazioni. È quindi anche un "front-end" verso altri strumenti matematici simili a GNU TeXmacs.
- MoinMoin è un sistema Wiki per la gestione della conoscenza.
- Documentazione usando Sphinx.
- Uno strumento automatico di testing, che consente la prova sul computer di un utente finale.
- Benché non direttamente supportato, SageMath può essere invocato all'interno di Mathematica.[4] Un notebook di Mathematica è disponibile per questa funzionalità.[5]
Sviluppo
[modifica | modifica wikitesto]
Durante lo sviluppo di SageMath William Stein si è reso conto che erano presenti una varietà di software matematici open-source scritti in diversi linguaggi di programmazione, come C, C++, Common Lisp, Fortran e Python.
Invece di "reinventare la ruota", SageMath (che è scritto principalmente in Python e Cython) contiene i diversi software matematici esistenti in un'unica interfaccia, per la quale la sintassi utilizzata è quella di Python. Inoltre sono state scritte centinaia di migliaia righe di codice allo scopo di aggiungere nuove funzionalità e collegare le diverse componenti.[6]
SageMath è sviluppato da studenti e professionisti sia attraverso contributi volontari che sovvenzioni.[7]
Rilasci
[modifica | modifica wikitesto]Nella seguente tabella sono indicati solo gli sviluppi maggiori. SageMath segue una politica dei rilasci che prevede nuovi aggiornamenti ogni poche settimane o mesi. In totale sono state effettuati più di 300 rilasci, anche se ultimamente la frequenza sta diminuendo.[8]
| Version | Release Date | Description |
|---|---|---|
| 0.1 | Gennaio 2005 | Viene incluso PARI |
| 0.2–0.4 | Marzo-Luglio 2005 | Polinomi in più variabili, estensione della documentazione |
| 0.5–0.7 | Agosto-Settembre 2005 | Spazi Vettoriali, anelli |
| 0.8 | Ottobre 2005 | GAP, Singular |
| 0.9 | Novembre 2005 | Sono stati aggiunti Maxima e clisp |
| 1.0 | Febbraio 2006 | |
| 2.0 | Gennaio 2007 | |
| 3.0 | Aprile 2008 | Interacts, R interfaccia |
| 4.0 | Maggio 2009 | Supporto per Solaris 10 e OSX a 64bit |
| 5.0 | Maggio 2012[9] | Supporto per OSX Lion |
| 6.0 | Dicembre 2013 | Lo sviluppo di SageMath si è spostato su Git[10] |
| 7.0 | Gennaio 2016 | Miglioramenti nell'interfaccia grafica |
| 8.0 | Luglio 2017 | Prima versione con supporto completo a Microsoft Windows |
Software contenuti in SageMath
[modifica | modifica wikitesto]La filosofia di Sage è quella di utilizzare quando disponibili le esistenti librerie open source. Quindi prende in prestito da molti progetti nella realizzazione del lavoro finale.
| Algebra | GAP, Maxima, SINGULAR |
| Geometria Algebrica | SINGULAR |
| Precisione Aritmetica Arbitraria | GMP, MPFR, MPFI, NTL |
| Geometria Aritmetica | PARI/GP, NTL, mwrank, ecm |
| Calcolo | Maxima, SymPy, GiNaC |
| Combinatorio | Symmetrica, Sage-Combinat |
| Algebra Lineare | ATLAS, BLAS, LAPACK, NumPy, LinBox, IML, GSL |
| Teoria dei Grafi | NetworkX |
| Teoria dei Gruppi | GAP |
| Calcolo numerico | GSL, SciPy, NumPy, ATLAS |
| Teoria dei Numeri | PARI/GP, FLINT, NTL |
| Calcolo statistico | R, SciPy |
| Riga di Comando | IPython |
| Database | ZODB, Python Pickles, SQLite |
| Interfaccia grafica | Sage Notebook, jsmath |
| Grafiche | Matplotlib, Tachyon3d, GD Graphics Library, Jmol |
| Linguaggio di programmazione interattivo | Python |
| Networking | Twisted |
| Geometria Differenziale e Calcolo Tensoriale | Sage Manifolds[11] |
Licenza e disponibilità
[modifica | modifica wikitesto]SageMath è un software libero, rilasciato con licenza GNU General Public License. Può essere ottenuto in diverse maniere:
- Il codice sorgente può essere scaricato dalla pagina dei downloads., nella quale sono disponibili anche le versioni di sviluppo.
- Sono presenti file binari precompilati per Linux, OS X e Solaris (sia nella versione x86 che SPARC).
- È disponibile un Live CD per un utilizzo di SageMath anche su macchine che non hanno Linux, OS X o Solaris installati.
- Fino al 17 aprile 2015 era possibile utilizzare una versione online di SageMath su sagenb.org (archiviato dall'url originale il 30 aprile 2007)..
- È possibile utilizzare online una versione "single cell" di SageMath su sagecell.sagemath.org. o incorporare una "singe cell" in un qualunque sito web. È inoltre possibile creare dei link permanenti a SageMath utilizzando il single cell server.[12]
- È disponibile una nuova versione online di SageMath su cloud.sagemath.com.. Su questa versione è inoltre possibile compilare documenti in LaTeX, utilizzare un terminale Linux e un notebook Jupyter.
- È disponibile nelle repo delle distro Debian-derivate
Esempi interfaccia di comando
[modifica | modifica wikitesto]Analisi
[modifica | modifica wikitesto]x,a,b,c = var('x,a,b,c')
log(sqrt(a)).simplify_log() # returns log(a)/2
log(a/b).simplify_log() # returns log(a) - log(b)
sin(a+b).simplify_trig() # returns cos(a)*sin(b) + sin(a)*cos(b)
cos(a+b).simplify_trig() # returns cos(a)*cos(b) - sin(a)*sin(b)
(a+b)ˆ5 # returns (b + a)ˆ5
expand((a+b)ˆ5) # returns bˆ5 + 5*a*bˆ4 + 10*aˆ2*bˆ3 +
# 10*aˆ3*bˆ2 + 5*aˆ4*b + aˆ5
limit((xˆ2+1)/(2+x+3*xˆ2), x=infinity) # returns 1/3
limit(sin(x)/x, x=0) # returns 1
diff(acos(x),x) # returns -1/sqrt(1 - xˆ2)
f = exp(x)*log(x)
f.diff(x,3) # returns e^x*log(x) + 3*e^x/x - 3*e^x/x^2 + 2*e^x/x^3
solve(a*x^2 + b*x + c, x) # returns [x == (-sqrt(b^2 - 4*a*c) - b)/(2*a),
# x == (sqrt(b^2 - 4*a*c) - b)/(2*a)]
f = xˆ2 + 432/x
solve(f.diff(x)==0,x) # returns [x == 3*sqrt(3)*I - 3,
# x == -3*sqrt(3)*I - 3, x == 6]
Equazioni differenziali
[modifica | modifica wikitesto]t = var('t') # definisce la variable t
x = function('x',t) # definisce che x deve essere una funzione della variabile t
DE = lambda y: diff(y,t) + y - 1
desolve(DE(x(t)), [x,t]) # restituisce '%e^-t*(%e^t+%c)'
Algebra lineare
[modifica | modifica wikitesto]A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
y = vector([0,-4,-1])
A.solve_right(y) # returns (-2, 1, 0)
A.eigenvalues() # returns [5, 0, -1]
B = Matrix([[1,2,3],[3,2,1],[1,2,1]])
B.inverse() # returns [ 0 1/2 -1/2]
# [-1/4 -1/4 1]
# [ 1/2 0 -1/2]
# Call numpy for the Moore-Penrose pseudo-inverse,
# since Sage does not support that yet.
import numpy
C = Matrix([[1 , 1], [2 , 2]])
matrix(numpy.linalg.pinv(C.numpy())) # returns [0.1 0.2]
# [0.1 0.2]
Teoria dei Numeri
[modifica | modifica wikitesto]prime_pi(1000000) # returns 78498, the number of primes less than one million
E = EllipticCurve('389a') # construct an elliptic curve from its Cremona label
P, Q = E.gens()
7*P + Q # returns (2869/676 : -171989/17576 : 1)
Note
[modifica | modifica wikitesto]- ^ Sage documentation.
- ^ Sage Interact functionality, su wiki.sagemath.org. URL consultato l'11 aprile 2008.
- ^ The TeX Catalogue OnLine, Entry for sagetex, Ctan Edition, su ctan.org. URL consultato il 2 maggio 2010 (archiviato dall'url originale il 2 febbraio 2009).
- ^ UsingSage (archiviato dall'url originale l'8 luglio 2012). Calling Sage from Mathematica
- ^ http://facstaff.unca.edu/mcmcclur/Mathematica/Sage/UsingSage.nb Archiviato il 19 luglio 2011 in Internet Archive. A Mathematica notebook to call Sage from Mathematica.
- ^ days7 - Sage Wiki, su wiki.sagemath.org, 14 novembre 2008. URL consultato il 9 dicembre 2013.
- ^ Sage – Acknowledgement, su sagemath.org. URL consultato il 13 luglio 2010.
- ^ SageMath Download - src-old, su sagemath.org. URL consultato il 17 luglio 2011.
- ^ sage-5.0.txt (TXT) [collegamento interrotto], su sagemath.org. URL consultato il 17 maggio 2012.
- ^ Installing and using SageMath just got even easier, su drvinceknight.blogspot.com. URL consultato il 12 luglio 2014.
- ^ SageManifolds: home.
- ^ About the SageMath Cell Server, su sagecell.sagemath.org. URL consultato il 9 dicembre 2013.
Voci correlate
[modifica | modifica wikitesto]- Free Software/Open Source e Freeware relativi:
- Software commerciali simili
Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su Sage
Wikimedia Commons contiene immagini o altri file su Sage
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Project home page, su sagemath.org.
- (EN) A Brief Introduction to Sage (PDF) [collegamento interrotto], su sagemath.org.
- (EN) Online Sage in web-browser, su cloud.sagemath.com.
- (EN) Sage Reference Manual, su sagemath.org. URL consultato il 4 maggio 2019 (archiviato dall'url originale il 23 luglio 2008).
- (EN) Free software brings affordability, transparency to mathematics, su physorg.com.









