Questa voce o sezione sull'argomento analisi matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

---

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti.

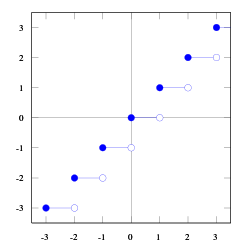
In matematica, la funzione parte intera, nota anche come funzione floor (dalla parola inglese floor che significa "pavimento"), è la funzione che associa ad ogni numero reale ${\displaystyle x}$ il più grande intero minore o uguale a ${\displaystyle x}$. La funzione parte intera è solitamente indicata con ${\displaystyle \lfloor x\rfloor }$ o ${\displaystyle [x]}$.

La funzione mantissa, definita come ${\displaystyle x-\lfloor x\rfloor }$, anche scritta come ${\displaystyle x}$ mod 1, oppure ${\displaystyle \{x\}}$, è chiamata la parte frazionaria di ${\displaystyle x}$. Ogni frazione ${\displaystyle x}$ può essere scritta come un numero misto, cioè la somma di un intero e una frazione propria. La funzione floor e la funzione parte frazionaria estendono questa decomposizione a tutti i numeri reali.

Qualche proprietà della funzione parte intera.

• Si ha

${\displaystyle \lfloor x\rfloor =\max \,\{k\in \mathbb {Z} :k\leq x\},}$

${\displaystyle \lfloor x\rfloor \leq x<\lfloor x\rfloor +1,}$

con l'uguaglianza nella parte sinistra che vale se e solo se ${\displaystyle x}$ è un intero.

• La funzione parte intera è idempotente:

${\displaystyle \lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor .}$

• Per ogni intero ${\displaystyle k}$ e ogni numero reale ${\displaystyle x}$,

${\displaystyle \lfloor k+x\rfloor =k+\lfloor x\rfloor .}$

• Per ogni ${\displaystyle x}$ e ${\displaystyle y}$ reali,

${\displaystyle \lfloor x\pm y\rfloor =\lfloor x\rfloor \pm \lfloor y\rfloor +\lfloor x\pm y-\lfloor x\rfloor \mp \lfloor y\rfloor \rfloor .}$

• Per ogni intero ${\displaystyle k}$ e ogni numero reale ${\displaystyle x}$,

${\displaystyle \lfloor kx\rfloor =k\lfloor x\rfloor +\lfloor kx-k\lfloor x\rfloor \rfloor .}$

• Per ogni ${\displaystyle x}$ e ${\displaystyle y}$ reali,

${\displaystyle \lfloor xy\rfloor =\lfloor x\rfloor \lfloor y\rfloor +\lfloor xy-\lfloor x\rfloor \lfloor y\rfloor \rfloor .}$

• Per ogni numero reale non intero ${\displaystyle x}$ si ha:

${\displaystyle \lfloor -x\rfloor =-\lfloor x\rfloor -1.}$

• L'ordinario arrotondamento di un numero ${\displaystyle x}$ all'intero più vicino può essere espresso come ${\displaystyle \lfloor x+0,5\rfloor }$.
• La funzione parte intera non è continua, ma è semi-continua. Essendo una funzione costante a tratti , la sua derivata è zero quando esiste, cioè per tutti i valori che non sono interi.
• Se ${\displaystyle x}$ è un numero reale e ${\displaystyle n}$ un intero, si ha ${\displaystyle n\leq x}$ se e solo se ${\displaystyle n\leq \lfloor x\rfloor .}$ In linguaggio ricercato, la funzione parte intera fa parte di una connessione di Galois; è l'aggiunta superiore della funzione che immerge gli interi nei reali.
• Usando la funzione floor, si possono produrre diverse formule per calcolare i numeri primi che sono esplicite ma non utilizzabili nella pratica.
• Il teorema di Beatty afferma che ogni numero irrazionale partiziona i numeri naturali in due sequenze tramite la funzione floor.

Una funzione strettamente correlata è la parte intera superiore, nota anche come funzione ceil (dalla parola inglese ceiling che significa "soffitto", contrapposta a floor, "pavimento"), definita nel modo seguente: per ogni numero reale ${\displaystyle x}$, ceil(${\displaystyle x}$) è il più piccolo intero non minore di ${\displaystyle x}$. Per esempio, ceil(2,3) = 3, ceil(2) = 2 e ceil(−2,3) = -2. La funzione ceiling è anche indicata con ${\displaystyle \lceil x\rceil }$. È facile provare che

${\displaystyle \lceil x\rceil =-\lfloor -x\rfloor }$

e che

${\displaystyle x\leq \lceil x\rceil <x+1.}$

Se poi x non è un intero si ha

${\displaystyle \lceil x\rceil -\lfloor x\rfloor =1.}$

Per ogni intero k, abbiamo anche che:

${\displaystyle \lfloor k/2\rfloor +\lceil k/2\rceil =k.}$

Se m e n sono interi positivi primi fra di loro, allora

${\displaystyle \sum _{i=1}^{n-1}\lfloor im/n\rfloor =(m-1)(n-1)/2.}$

Se ${\displaystyle x}$ è un numero irrazionale, allora le parti frazionarie ${\displaystyle nx{\bmod {1}}}$, dove ${\displaystyle n}$ varia fra gli interi positivi, sono distribuite uniformemente nell'intervallo aperto ${\displaystyle (0,1)}$. Questa affermazione può essere resa più precisamente in molti modi, uno dei quali afferma:

${\displaystyle \int _{0}^{1}f(t)\;dt=\lim _{N\to \infty }{\frac {1}{N}}\sum _{n=1}^{N}f(nx{\bmod {1}}),}$

per ogni funzione continua a valori reali ${\displaystyle f\colon [0,1]\to \mathbb {R} }$ (si vedano limite, integrale e teorema dell'equidistribuzione).

Seguendo il principio generale dell'approssimazione diofantea scoperto da Hermann Weyl, questa proprietà è equivalente a qualcosa che è molto più facile da controllare: ossia che le somme

${\displaystyle \sum \limits _{n=0}^{N}e^{2\pi iknx},}$

per ${\displaystyle k\in \mathbb {N} }$ sono O(N). Poiché sono progressioni geometriche, questo può essere provato in maniera abbastanza diretta. La condizione che ${\displaystyle x}$ sia irrazionale implica che

${\displaystyle \sin(\pi kx)\neq 0.}$

Lo stesso argomento in dettaglio: Troncamento (matematica).

Mentre la funzione parte intera genera solamente numeri interi, il troncamento, cioè il "tagliare fuori le cifre", può essere effettuato a qualsiasi posizione specificata, non solo dopo la cifra delle unità.

Le funzioni parte intera superiore e inferiore sono normalmente indicate con parentesi quadre, chiuse e aperte, in cui le linee orizzontali superiori (per la funzione parte intera inferiore, floor) o inferiori (per la funzione parte intera superiore, ceiling) sono mancanti. Per esempio nel sistema di composizione editoriale LaTeX questi simboli possono essere realizzati con i comandi \lfloor, \rfloor, \lceil e \rceil.

• Wikimedia Commons contiene immagini o altri file su floor e ceiling

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica