Questa voce o sezione sull'argomento geometria non cita le fonti necessarie o quelle presenti sono insufficienti.

---

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Si presenta la generica omotetia nel piano complesso di centro ${\displaystyle C_{0}(x_{0},y_{0})}$ e rapporto ${\displaystyle a}$, con ${\displaystyle a}$ numero reale diverso da zero e ${\displaystyle C_{0}}$ punto del piano complesso (si veda numeri complessi e punti del piano cartesiano).

Sia ${\displaystyle C_{0}=P(z_{0})}$ il punto corrispondente al numero complesso ${\displaystyle z_{0}=x_{0}+iy_{0}}$, e sia ${\displaystyle a}$ un numero reale diverso da ${\displaystyle 0}$ e da ${\displaystyle 1}$. L'omotetia ${\displaystyle \omega _{C_{0},a}}$ di centro ${\displaystyle C_{0}}$ e rapporto ${\displaystyle a}$, è la trasformazione che associa ad ogni punto ${\displaystyle P=P(z)}$, corrispondente del numero complesso ${\displaystyle z}$, il punto ${\displaystyle P'=P'(z')}$, corrispondente del numero complesso ${\displaystyle z'}$, tale che:

${\displaystyle {\vec {C_{0}P'}}=a{\vec {C_{0}P}}.}$

Dal momento che

${\displaystyle {\vec {C_{0}P}}=z-z_{0},\quad {\vec {C_{0}P'}}=z'-z_{0},}$

si ha che

${\displaystyle z'-z_{0}=a\left(z-z_{0}\right).}$

Quindi, introducendo ${\displaystyle b:=(1-a)z_{0}}$, la scrittura complessa dell'omotetia è:

${\displaystyle {\begin{aligned}\omega _{C_{0},a}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=az+b=a\rho e^{i\theta }+b.\end{aligned}}}$

In modo particolare l'omotetia ${\displaystyle \omega _{O,a}}$ di centro l'origine degli assi ${\displaystyle O}$ e rapporto ${\displaystyle a}$, è la trasformazione

${\displaystyle {\begin{aligned}\omega _{O,a}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=az=a\rho e^{i\theta }=a\rho \left(\cos \theta +i\sin \theta \right),\end{aligned}}}$

ove si è posto

${\displaystyle z=\rho \left(\cos \theta +i\sin \theta \right).}$

Osserviamo inoltre come opera la trasformazione in base al segno del numero ${\displaystyle a}$:

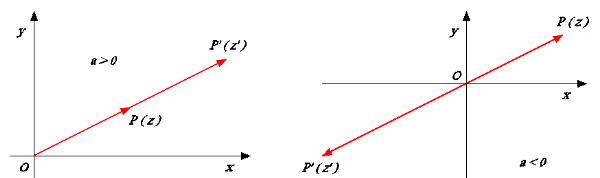
Quindi:

moltiplicare il numero complesso ${\displaystyle z}$ per un numero reale ${\displaystyle a}$ non nullo e diverso da ${\displaystyle 1}$ equivale ad applicare al punto ${\displaystyle P(z)}$ l'omotetia di rapporto ${\displaystyle a}$.

Si determina la scrittura complessa dell'omotetia di centro ${\displaystyle C_{0}(-2,4)}$ e rapporto ${\displaystyle 3}$.

Il numero complesso corrispondente a questo punto è ${\displaystyle z_{0}=-2+4i}$.

Quindi, ricordando che l'omotetia si ottiene con ${\displaystyle z'-z_{0}=a(z-z_{0})}$, si ha che

${\displaystyle z'-(-2+4i)=3(z-(-2+4i))}$ cioè ${\displaystyle z'=3z+4-8i}$.

• Omotetia
• Trasformazione geometrica piana

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica