
In matematica, e più precisamente in teoria dei nodi, un nodo primo è un nodo che non può essere "decomposto" in nodi più semplici, in analogia con la nozione di numero primo.
I nodi primi sono quindi i mattoni fondamentali della teoria dei nodi.
Definizione
[modifica | modifica wikitesto]Un nodo non banale è primo se non è ottenibile come somma connessa
di due nodi non banali.
Nella teoria dei nodi vi è un teorema di fattorizzazione analogo al teorema fondamentale dell'aritmetica, che asserisce che ogni nodo è ottenibile in modo unico come somma connessa di alcuni nodi primi. Per questo motivo i nodi primi hanno un ruolo centrale nella teoria dei nodi: una loro classificazione è stato da sempre il tema centrale della teoria fin dalla fine del XIX secolo.
In analogia con i numeri primi, si richiede nella definizione che il nodo banale non sia primo (il numero 1 infatti non è primo).
I nodi primi più semplici
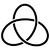
[modifica | modifica wikitesto]I nodi primi sono generalmente descritti tramite diagrammi, con ordine crescente di incroci. Il nodo primo più semplice in questa descrizione è il nodo a trifoglio con 3 incroci, seguito dal nodo a otto con quattro incroci. La tabella seguente mostra il numero di nodi primi con incroci.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Numero di nodi primi con incroci | 0 | 0 | 1 | 1 | 2 | 3 | 7 | 21 | 49 | 165 |
Nella tabella due nodi ottenuti tramite una riflessione lungo un piano vengono considerati equivalenti: non si tiene conto cioè della chiralità (esistono ad esempio "due versioni" del nodo a trifoglio, e qui ne viene contata una sola).
Nella tabella seguente sono disegnati tutti i nodi primi ottenibili con 6 incroci:
| 3 | 4 | 5 | 5 | 6 | 6 | 6 |
 |
 |
 |
 |

|
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su nodo primo
Wikimedia Commons contiene immagini o altri file su nodo primo
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Prime Knot su MathWorld.











