Nel contesto dei circuiti quantistici sono usate comunemente per i calcoli diverse porte quantistiche (o porte logiche quantistiche). Di seguito sono riportate delle tabelle che elencano le varie porte quantistiche unitarie riportando il loro nome comune, il modo in cui sono rappresentate e alcune loro proprietà. Le versioni controllate o coniugate hermitiane di alcune di queste porte potrebbero non essere presenti nell'elenco.
| Nomi
|
# qubit
|
Simboli dell'operatore
|
Matrice
|
Circuito
|
Proprietà
|
Note
|
|
|
1 (qualsiasi)
|
 , ,  , 𝟙 , 𝟙
|

|

oppure

|
|
[1]
|
|
|
1 (qualsiasi)
|
 , ,  , , 
|

|

|
- Parametri continui:
 (periodo (periodo  ) )
- Forma esponenziale:

|
[1]
|
La porta identità è l'operazione di identità  , il più delle volte questa porta non è indicata negli schemi circuitali, ma è utile per descrivere alcuni risultati matematici.
, il più delle volte questa porta non è indicata negli schemi circuitali, ma è utile per descrivere alcuni risultati matematici.
Spesso è descritta come un "ciclo di attesa" e un NOP.[1]
La porta global phase introduce una fase globale  all'intero stato quantistico del qubit. Uno stato quantistico è definito in modo univoco fino ad una fase. A causa della legge di Born, un phase factor non ha effetto sul risultato di una misurazione:
all'intero stato quantistico del qubit. Uno stato quantistico è definito in modo univoco fino ad una fase. A causa della legge di Born, un phase factor non ha effetto sul risultato di una misurazione:  per ogni
per ogni  .
.
Poiché  quando la porta global phase viene applicata ad un singolo qubit in un registro quantistico, la fase globale dell'intero registro viene modificata.
quando la porta global phase viene applicata ad un singolo qubit in un registro quantistico, la fase globale dell'intero registro viene modificata.
Inoltre, 
Queste porte possono essere estese a qualsiasi numero di qubit o qudit.
Questa tabella include le porte di Clifford comunemente usate per i qubit.[1][2][3]
| Nomi
|
# qubits
|
Simbolo dell'operatore
|
Matrice
|
Circuito
|
Alcune poprietà
|
Note
|
|
|
1
|

|

|

oppure
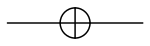
|
- Hermitiana
- Gruppo di Pauli
- Senza traccia
- Involutoria
|
[1][4]
|
|
|
1
|

|

|

|
- Hermitiana
- Gruppo di Pauli
- Senza traccia
- Involutoria
|
[1][4]
|
|
|
1
|

|

|

|
- Hermitiana
- Gruppo di Pauli
- Senza traccia
- Involutoria
|
[1][4]
|
- phase S
- radice quadrata di Z
|
1
|

|

|

|
|
[1][4]
|
- radice quadrata di X
- radice quadrata di NOT
|
1
|
 , ,  , , 
|

|

|
|
[1][5]
|
|
|
1
|

|

|

|
- Hermitiana
- Senza traccia
- Involutoria
|
[1][4]
|
|
|
2
|
 , , 
|


|

|
Implementazione:
|
[1][4]
|
- anticontrolled-NOT
- anticontrolled-X
- zero control
- control-on-0-NOT
- reversible exclusive NOR
|
2
|
 , , ![{\textstyle {\text{controlled[0]-NOT}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666bd05c87c61de2047eb0613ea0730f86667f31) , , 
|

|

|
|
[1]
|
- controlled-Z
- controlled sign flip
- controlled phase flip
|
2
|
 , ,  , ,  , , 
|

|

|
- Hermitiana
- Involutoria
- Simmetrica
Implementazione:
|
[1][4]
|
|
|
2
|

|

|
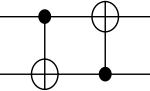
|
|
[6]
|
|
|
2
|

|

|

oppure

|
- Hermitiana
- Involutoria
- Simmetrica
|
[1][4]
|
|
|
2
|

|

|

oppure

|
- Unitaria speciale
- Simmetrica
|
[1]
|
|
|
2
|

|

|
|
- Unitaria speciale
- Simmetrica
|
[7]
|
Altre porte di Clifford, comprese quelle di dimensioni superiori, non sono state incluse ma per definizione possono essere generate utilizzando  e
e  .
.
Si noti che se una porta A di Clifford non è nel gruppo di Pauli,  o controlled-A non sono tra le porte di Clifford.
o controlled-A non sono tra le porte di Clifford.
Va specificato inoltre che l'insieme delle porte di Clifford non è un insieme di porte quantistiche universali.
| Nomi
|
# qubit
|
Simbolo dell'operatore
|
Matrice
|
Schema circuitale
|
Proprietà
|
Note
|
|
|
1
|

|

|

|
- Parametri continui:
 (periodo (periodo  ) )
|
[8][9][10]
|
- phase T
- porta π/8
- radice quarta di Z
|
1
|
 , , ![{\textstyle {\sqrt[{4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b2ff605c151630e78170afaaae7365137570604)
|

|
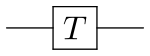
|
|
[1][4]
|
|
|
2
|

|

|

|
- Parametri continui:
 (periodo (periodo  ) )
- Simmetrica
|
[10]
|
|
|
2
|

|

|

|
|
[4]
|
Quella dello spostamento di fase è una famiglia di porte a singolo qubit che mappano gli stati di base  e
e  . La probabilità di misurare un
. La probabilità di misurare un  o un
o un  rimane invariata dopo aver applicato questa porta, tuttavia modifica la fase dello stato quantistico. Ciò equivale a tracciare un cerchio orizzontale (una linea di latitudine) o ad applicare una rotazione lungo l'asse z sulla sfera di Bloch di
rimane invariata dopo aver applicato questa porta, tuttavia modifica la fase dello stato quantistico. Ciò equivale a tracciare un cerchio orizzontale (una linea di latitudine) o ad applicare una rotazione lungo l'asse z sulla sfera di Bloch di  radianti. Un esempio comune è la porta a T dove
radianti. Un esempio comune è la porta a T dove  (storicamente noto come il
(storicamente noto come il  gate), il gate di fase. Si noti che alcune porte di Clifford sono casi particolari di porta phase shift:
gate), il gate di fase. Si noti che alcune porte di Clifford sono casi particolari di porta phase shift:

L'argomento della porta phase shift è in U(1) e la porta induce una rotazione di fase in U(1) lungo lo stato di base specificato (ad es.  fa ruotare la fase attorno a
fa ruotare la fase attorno a  . L'estensione di
. L'estensione di  ad una rotazione su una fase generica di entrambi gli stati base di un sistema quantistico a 2 livelli (un qubit) può essere eseguita con un circuito in serie:
ad una rotazione su una fase generica di entrambi gli stati base di un sistema quantistico a 2 livelli (un qubit) può essere eseguita con un circuito in serie:

Quando  questa porta è l'operatore di rotazione
questa porta è l'operatore di rotazione  e se
e se  è un phase shift. [N 1] [N 2]
è un phase shift. [N 1] [N 2]
Storicamente il nome " " della porta T di deriva dall'identità
" della porta T di deriva dall'identità  , dove
, dove  .
.
Porte a sfasamento arbitrarie a qubit singolo  sono disponibili nativamente per processori quantistici transmon attraverso la temporizzazione degli impulsi di controllo a microonde.[11] Può essere spiegato in termini di cambio di frame.[12]
sono disponibili nativamente per processori quantistici transmon attraverso la temporizzazione degli impulsi di controllo a microonde.[11] Può essere spiegato in termini di cambio di frame.[12]
Come con qualsiasi porta a qubit singolo, è possibile creare una versione controllata della porta phase shift. Per quanto riguarda la base computazionale, la porta controlled phase a 2 qubit è: sposta la fase con  solo se agisce sullo Stato
solo se agisce sullo Stato  :
:

La porta controlled-Z (o CZ) è il caso particolare in cui  .
.
La porta controlled-S è il caso controlled- in cui
in cui  ed è una porta comunemente usata.[4]
ed è una porta comunemente usata.[4]
| Nomi
|
# qubit
|
Simboli dell'operatore
|
Forma esponenziale
|
Matrice
|
Schema circuitale
|
Proprietà
|
Note
|
|
|
1
|

|

|

|

|
- Unitaria speciale
- Parametri continui:
 (periodo (periodo  ) )
|
[1][4]
|
|
|
1
|

|

|

|
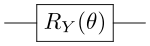
|
- Unitaria speciale
- Parametri continui:
 (periodo (periodo  ) )
|
[1][4]
|
|
|
1
|

|

|

|
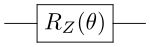
|
- Unitaria speciale
- Parametri continui:
 (periodo (periodo  ) )
|
[1][4]
|
Gli operatori di rotazione  e
e  sono le matrici di rotazione analogiche in tre assi cartesiani di SO(3), gli assi sulla proiezione della sfera di Bloch.
sono le matrici di rotazione analogiche in tre assi cartesiani di SO(3), gli assi sulla proiezione della sfera di Bloch.
Poiché le matrici di Pauli sono correlate al generatore di rotazioni, questi operatori di rotazione possono essere scritti come esponenziali di matrice con matrici di Pauli per argomento. Qualunque matrice unitaria  in SU(2) può essere scritta come un prodotto (cioè un circuito in serie) di al più tre porte di rotazione. Si noti che per i sistemi a due livelli come qubit e spinori, queste rotazioni hanno un periodo di 4π. Una rotazione di 2π (360 gradi) restituisce lo stesso vettore di stato con una fase diversa.[13]
in SU(2) può essere scritta come un prodotto (cioè un circuito in serie) di al più tre porte di rotazione. Si noti che per i sistemi a due livelli come qubit e spinori, queste rotazioni hanno un periodo di 4π. Una rotazione di 2π (360 gradi) restituisce lo stesso vettore di stato con una fase diversa.[13]
Abbiamo anche  e
e  per tutti
per tutti 
Le matrici di rotazione sono così legate alle matrici di Pauli: 
È possibile calcolare l'azione aggiuntiva delle rotazioni sul vettore di Pauli:

Prendendo il prodotto scalare di qualsiasi vettore unitario con la formula sopracitata, si genera l'espressione di ogni singola porta qubit quando infrapposta tra porte di rotazione adiacenti. Ad esempio, si può dimostrare che  . Inoltre, con la relazione anticommutativa abbiamo:
. Inoltre, con la relazione anticommutativa abbiamo:  .
.
Gli operatori di rotazione hanno identità interessanti. Per esempio,  e
e  Inoltre, usando le relazioni anticommutative abbiamo:
Inoltre, usando le relazioni anticommutative abbiamo:  e
e 
Si può trasformare phase shift e global phases poiché abbiamo anche l'identità  .
.
La porta  rappresenta una rotazione di π/2 attorno all'asse x alla sfera di Bloch:
rappresenta una rotazione di π/2 attorno all'asse x alla sfera di Bloch:  .
.
Esistono anche delle porte di operatori di rotazione simili per SU(3) che utilizzano le matrici di Gell-Mann. Questi sono gli operatori di rotazione per qutrits.
Le porte di accoppiamento di Ising o di interazione di Heisenberg Rxx, Ryy e Rzz sono porte a 2 qubit implementate in modo nativo in alcuni computer quantistici a trappole ioniche (sono correlate alle porte Mølmer–Sørensen).[14][15] Si noti che:
 .
.
La portaCNOT può essere ulteriormente scomposta come prodotti di operatori di rotazione e esattamente una porta di accoppiamento di Ising, ad esempio:

La porta SWAP può essere costruita con altre porte, ad esempio utilizzando le porte di accoppiamento di Ising:  .
.
| Nomi
|
# qubit
|
Simboli dell'operatore
|
Matrice
|
Schema circuitale
|
Proprietà
|
Note
|
|
|
2
|

|

|

|
|
[1]
|
- radice quadrata di swap immaginario
|
2
|

|

|
|
|
[10]
|
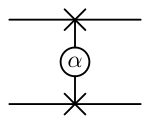
- swap (elevato a esponente)
|
2
|

|

|
|
- Parametri continui:
 (periodo (periodo  ) )
|
[1]
|
|
|
3
|
 , , 
|

|

oppure

|
- Hermitiana
- Involutiva
- Porta reversibile funzionalmente completa per l'algebra booleana
|
[1][4]
|
La porta  esegue a metà uno scambio di due qubit (vedi porte di Clifford). È universale in modo tale che qualsiasi porta multi-qubit possa essere costruita con sole
esegue a metà uno scambio di due qubit (vedi porte di Clifford). È universale in modo tale che qualsiasi porta multi-qubit possa essere costruita con sole  e porte a qubit singolo. La porta
e porte a qubit singolo. La porta  non è tuttavia maximally entangling; ovvero deve essere applicata più volte per produrre uno stato di Bell dagli stati del prodotto. La porta
non è tuttavia maximally entangling; ovvero deve essere applicata più volte per produrre uno stato di Bell dagli stati del prodotto. La porta  compare naturalmente nei sistemi che sfruttano l'interazione di scambio.[1][16]
compare naturalmente nei sistemi che sfruttano l'interazione di scambio.[1][16]
Per i sistemi con interazioni Ising-like, a volte è più naturale introdurre lo scambio immaginario[17] o iSWAP.[18][19] Si noti che  e
e  , o più in generale
, o più in generale ![{\displaystyle {\sqrt[{n}]{i{\mbox{SWAP}}}}=R_{xx}(-\pi /2n)R_{yy}(-\pi /2n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f10366d0d56f5eff91c562190970f5c654c15992) per tutti i reali n tranne 0.
per tutti i reali n tranne 0.
SWAP α si manifesta naturalmente nei computer quantistici spintronici.[1]
La porta di Fredkin (anche CSWAP o CS gate), dal nome di Edward Fredkin, è un gate a 3 bit che esegue uno controlled-swap ed è universale per la computazione classica. Gode, inoltre, dell'utile proprietà per cui il numero di 0 e di 1 vengono sempre conservati; il che nel modello della palla da biliardo significa che lo stesso numero di palline viene emesso come input.
| Nomi
|
# qubits
|
Simboli dell'operatore
|
Matrice
|
Schema circuitale
|
Proprietà
|
Origine del nome
|
Note
|
- rotazione singola di qubit generale
|
1
|

|

|
|
- Implementa una rotazione singola di qubit
- Parametri continui:
 (periodo (periodo  ) )
|
Porta U in OpenQASM [N 3]
|
[10]
|
|
|
2
|

|

|
|
- Implementa una rotazione arbitraria di qubit controllata
- Porta quantistica universale
- Parametri continui:
 (periodo (periodo  ) )
|
Adriano Barenco
|
[1]
|
|
|
2
|

|

|
|
- Unitaria speciale
- Forma esponenziale:
![{\displaystyle \exp \left[i{\frac {\pi }{8}}(2X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e291eb824b8455eb9a3f59bf9084f5aaa24535)
|
University of California Berkeley[20]
|
[1]
|
- controlled-V,
- radice quadrata di NOT controllata
|
2
|
 
|

|
|
|
|
[21]
|
- core entangling
- scomposizione canonica
|
2
|
 , , 
|

|
|
- Unitaria speciale
- Porta quantistica universale
- Forma esponenziale:
![{\displaystyle \exp \left[i(aX\otimes X+bY\otimes Y+cZ\otimes Z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10fddc558772c4ace4b390095ac1c5cecddf273)
- Parametri continui:
 (period (period  ) )
|
|
[1]
|
- Dagoberto
- Dagwood Bumstead
|
2
|

|

|
|
- Unitaria speciale
- Forma esponenziale:
![{\displaystyle \exp \left[-i{\frac {3\pi }{16}}(X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bdec91d774e918820d8b3a2abbe9ce13939a7cf)
|
Personaggio della striscia a fumetti Blondie e Dagoberto[22]
|
[22][23]
|
|
|
2
|

|

|
|
|
|
[24]
|
|
|
2
|
 , , 
|

|
|
- Unitaria speciale
- Parametri continui:
 (period (period  ) )
|
|
[25]
|
|
|
2
|
 , , 
|

|
|
- Unitaria speciale
- Forma esponenziale:
![{\displaystyle \exp \left[-i{\frac {\theta }{2}}(Y\otimes X-X\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e807329af5f546f7c2f758c153dce7f0d4c79e93)
- Parametri continui:
 (period (period  ) )
|
Rotazioni di Givens
|
[26]
|
|
|
2
|

|

|
|
|
|
[1]
|
|
|
2
|
 , , 
|

|
|
|
Processore Sycamore di Google
|
[27]
|
|
|
3
|
 , , 
|

|
|
- Parametri continui:
 (period (period  ) )
- Porta quantistica universale
|
David Deutsch
|
[1]
|
- Margolus
- Toffoli semplificata
|
3
|
 , , 
|

|

|
- Hermitiana
- Involutoria
- Unitaria speciale
- Porta reversibile funzionalmente completa per l'algebra booleana
|
Norman Margolus
|
[28][29]
|
|
|
3
|
 , ,
|

|

|
- Porta reversibile funzionalmente completa per l'algebra booleana
|
Asher Peres
|
[30]
|
|
|
3
|

|

|

|
- Hermitiana
- Involutoria
- Porta reversibile funzionalmente completa per l'algebra booleana
|
Tommaso Toffoli
|
[1][4]
|
- ^
 when
when  , dove il simbolo
, dove il simbolo  indica la matrice trasposta coniugata
indica la matrice trasposta coniugata
- ^ Anche:

- ^ La matrice qui mostrata è di openQASM 3.0
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad Colin P. Williams, 2011, ISBN 978-1-84628-887-6.
- ^ Quantum mechanical computers, vol. 16, 1986, DOI:10.1007/bf01886518, ISSN 0015-9018 (WC · ACNP).
- ^ Elementary gates for quantum computation, vol. 52, DOI:10.1103/physreva.52.3457, ISSN 1050-2947 (WC · ACNP), PMID 9912645, arXiv:quant-ph/9503016.
- ^ a b c d e f g h i j k l m n o p Quantum computation and quantum information, su worldcat.org. URL consultato il 28 agosto 2024.
- ^ W.N.N. Hung, Xiaoyu Song e Guowu Yang, Optimal synthesis of multiple output Boolean functions using a set of quantum gates by symbolic reachability analysis, in IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 25, n. 9, 2006-09, pp. 1652–1663, DOI:10.1109/TCAD.2005.858352. URL consultato il 28 agosto 2024.
- ^ Daniel Collins, Noah Linden e Sandu Popescu, Nonlocal content of quantum operations, in Physical Review A, vol. 64, n. 3, 7 agosto 2001, pp. 032302, DOI:10.1103/PhysRevA.64.032302. URL consultato il 28 agosto 2024.
- ^ (EN) Alba Cervera-Lierta, Exact Ising model simulation on a quantum computer, in Quantum, vol. 2, 21 dicembre 2018, pp. 114, DOI:10.22331/q-2018-12-21-114. URL consultato il 28 agosto 2024.
- ^ (EN) Anirban Pathak, Elements of Quantum Computation and Quantum Communication, Taylor & Francis, 20 giugno 2013, ISBN 978-1-4665-1792-9. URL consultato il 28 agosto 2024.
- ^ (EN) Noson S. Yanofsky e Mirco A. Mannucci, Quantum Computing for Computer Scientists, Cambridge University Press, 11 agosto 2008, ISBN 978-1-139-64390-0. URL consultato il 28 agosto 2024.
- ^ a b c d (EN) Daniel D. Stancil e Gregory T. Byrd, Principles of Superconducting Quantum Computers, John Wiley & Sons, 19 aprile 2022, ISBN 978-1-119-75074-1. URL consultato il 28 agosto 2024.
- ^ academic.oup.com, https://academic.oup.com/ptep/article/2015/9/093A02/1566391?login=false. URL consultato il 28 agosto 2024.
- ^ qiskit.org, https://qiskit.org/documentation/stubs/qiskit.circuit.library.PhaseGate.html#qiskit.circuit.library.PhaseGate.
- ^ 2008, pp. 127–128, ISBN 978-3-527-40601-2.
- ^ Chris Monroe, Trapped Ions: Condensed Matter (PDF).
- ^ Demonstration of a small programmable quantum computer with atomic qubits (PDF).
- ^ vol. 3, 2021, Bibcode:2021PhRvR...3a3113N, DOI:10.1103/PhysRevResearch.3.013113, arXiv:2008.09819.
- ^ (EN) vol. 2, 17 luglio 2020, DOI:10.1103/PhysRevResearch.2.033097, ISSN 2643-1564 (WC · ACNP), arXiv:2002.11728, https://oadoi.org/10.1103/PhysRevResearch.2.033097.
- ^ (EN) vol. 67, 10 marzo 2003, DOI:10.1103/PhysRevA.67.032301, ISSN 1050-2947 (WC · ACNP), arXiv:quant-ph/0209035, https://oadoi.org/10.1103/PhysRevA.67.032301.
- ^ (EN) vol. 94, 5 dicembre 2016, DOI:10.1103/PhysRevA.94.062304, ISSN 2469-9926 (WC · ACNP), arXiv:1606.00208, https://oadoi.org/10.1103/PhysRevA.94.062304.
- ^ (EN) vol. 93, DOI:10.1103/PhysRevLett.93.020502, ISSN 0031-9007 (WC · ACNP), PMID 15323888, https://oadoi.org/10.1103/PhysRevLett.93.020502.
- ^ (EN) ISBN 978-1-4665-1792-9, https://books.google.com/books?id=cEPSBQAAQBAJ.
- ^ a b (EN) M. AbuGhanem, Two-qubit Entangling Gate for Superconducting Quantum Computers, ID 4188257, Social Science Research Network, 1º gennaio 2021. URL consultato il 28 agosto 2024.
- ^ (EN) vol. 4, DOI:10.22331/q-2020-03-26-247, https://oadoi.org/10.22331/q-2020-03-26-247.
- ^ (EN) vol. 6, DOI:10.1038/ncomms7979, ISSN 2041-1723 (WC · ACNP), PMID 25923200, https://oadoi.org/10.1038/ncomms7979.
- ^ (EN) vol. 104, DOI:10.1103/PhysRevA.104.052417, ISSN 2469-9926 (WC · ACNP), https://oadoi.org/10.1103/PhysRevA.104.052417.
- ^ (EN) vol. 6, DOI:10.22331/q-2022-06-20-742, https://oadoi.org/10.22331/q-2022-06-20-742.
- ^ (EN) vol. 574, DOI:10.1038/s41586-019-1666-5, ISSN 1476-4687 (WC · ACNP), PMID 31645734, https://oadoi.org/10.1038/s41586-019-1666-5.
- ^ (EN) vol. 93, DOI:10.1103/PhysRevA.93.022311, ISSN 2469-9926 (WC · ACNP), https://oadoi.org/10.1103/PhysRevA.93.022311.
- ^ Guang Song e Andreas Klappenecker, The simplified Toffoli gate implementation by Margolus is optimal, in arXiv:quant-ph/0312225, 31 dicembre 2003. URL consultato il 28 agosto 2024.
- ^ Himanshu Thapliyal e Nagarajan Ranganathan, Design of Efficient Reversible Binary Subtractors Based on a New Reversible Gate, in 2009 IEEE Computer Society Annual Symposium on VLSI, 2009-05, pp. 229–234, DOI:10.1109/ISVLSI.2009.49. URL consultato il 28 agosto 2024.






































































![{\textstyle {\text{controlled[0]-NOT}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666bd05c87c61de2047eb0613ea0730f86667f31)




















![{\textstyle {\sqrt[{4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b2ff605c151630e78170afaaae7365137570604)

































































![{\displaystyle {\displaystyle \exp \left[-i{\frac {\phi }{4}}(X\otimes X+Y\otimes Y\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62625ec3fa194f5a0394722303e3bcb0038aec3f)


















![{\displaystyle {\sqrt[{n}]{i{\mbox{SWAP}}}}=R_{xx}(-\pi /2n)R_{yy}(-\pi /2n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f10366d0d56f5eff91c562190970f5c654c15992)








![{\displaystyle \exp \left[i{\frac {\pi }{8}}(2X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e291eb824b8455eb9a3f59bf9084f5aaa24535)






![{\displaystyle \exp \left[i(aX\otimes X+bY\otimes Y+cZ\otimes Z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10fddc558772c4ace4b390095ac1c5cecddf273)



![{\displaystyle \exp \left[-i{\frac {3\pi }{16}}(X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bdec91d774e918820d8b3a2abbe9ce13939a7cf)









![{\displaystyle \exp \left[-i{\frac {\theta }{2}}(Y\otimes X-X\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e807329af5f546f7c2f758c153dce7f0d4c79e93)


















