function S = DragonCurve(pattern,MaxRecursionLevel)
% DRAGONCURVE
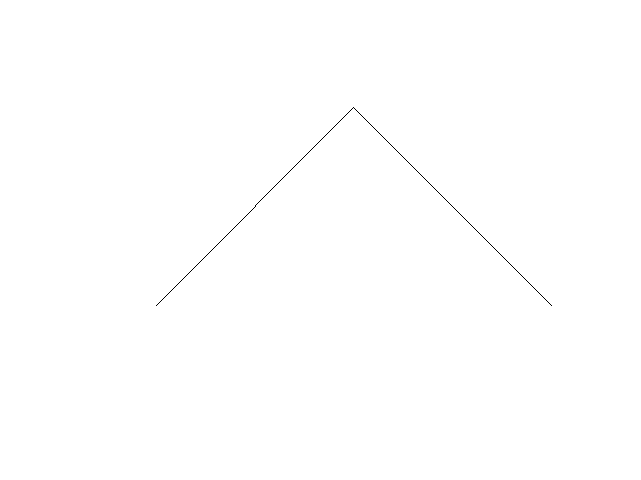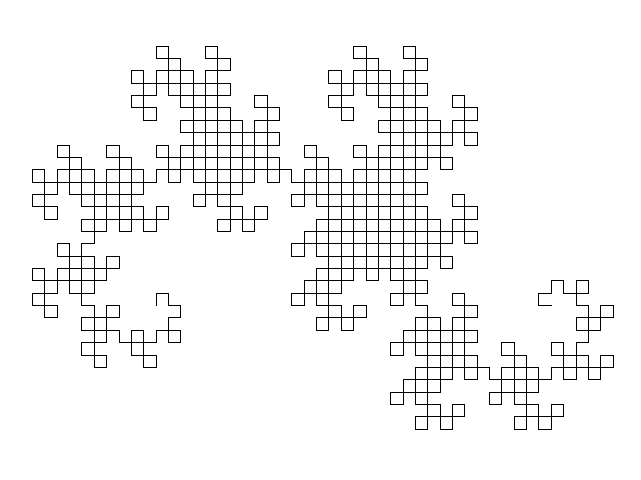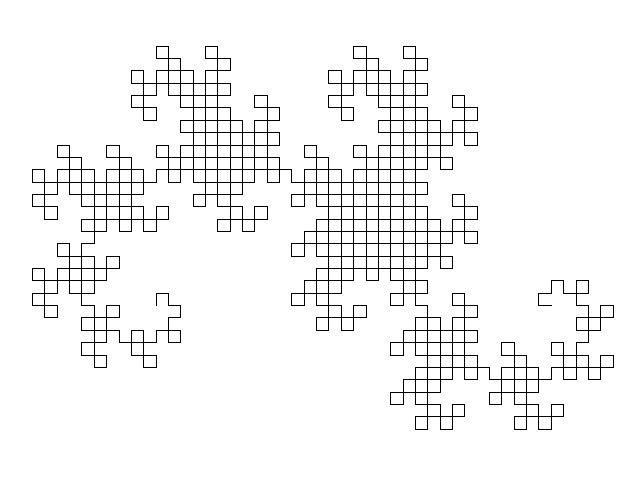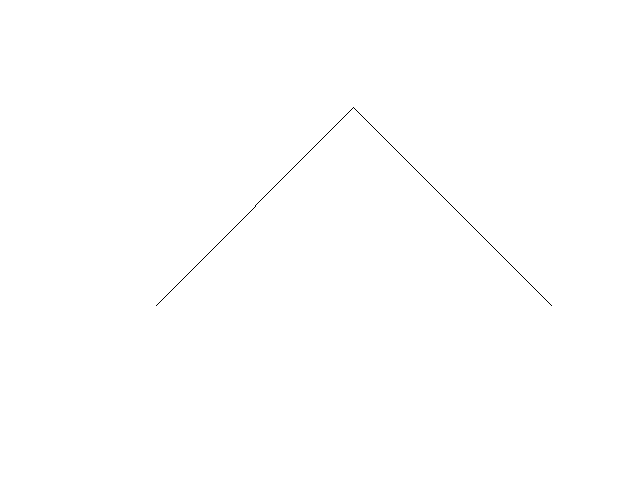
% This function generates a fractal curve called the dragon curve.
%
% A dragon curve is any member of a family of self-similar fractal curves,
% which can be approximated by recursive methods such as Lindenmayer
% systems.
%
% Inputs :
% - pattern : [Optional] Vector of complex that contain linear
% transformation to apply to each line segment
% - MaxRecursionLevel : [Optional] Maximum recusrion level
% Remember each time a new level is added, the
% number of line segments is doubled
% - options : [Optional] Structure with display option
%
% Outputs :
% - S : Structure that contains the line segment for each recursion level
% Just enter "plot(S(end).LineSeg,'k');" to plot the finest level
% generated
%
% See http://en.wikipedia.org/wiki/Dragon_curve
%
% 2011/07/10
% Guillaume Jacquenot
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if nargin < 3
options.plot = true;
options.generateGIFAnimate = true;
options.plotConvergence = false;
if nargin < 2
MaxRecursionLevel = 15;
if nargin < 1
pattern(1) = 0.5 * (1+1i);
pattern(2) = 0.5 * (1-1i);
end
end
end
S(MaxRecursionLevel) = struct('LineSeg',[]);
npat = numel(pattern);
S(1).LineSeg = [0;pattern(1:(npat-1));1];
for level = 2:MaxRecursionLevel;
delta = diff(S(level-1).LineSeg);
S(level).LineSeg = zeros(npat^level+1,1);
S(level).LineSeg(1:npat:end) = S(level-1).LineSeg;
S(level).LineSeg(2:4:end-3) = ...
S(level-1).LineSeg(1:2:end-2) + delta(1:2:end-1) * pattern(1);
S(level).LineSeg(4:4:end-1) = ...
S(level-1).LineSeg(2:2:end-1) + delta(2:2:end ) * pattern(2);
end
if options.plot || options.generateGIFAnimate
BBox = determineBoundingBox(S);
plotDragonCurve(S,BBox);
end
if options.generateGIFAnimate
cmd = generateGIFAnimationCommand(MaxRecursionLevel);
eval(cmd);
end
if options.plotConvergence
plot_Convergence_Evolution(S);
end
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plotDragonCurve(S,BBox)
figure('Color','w');
hold on
box on
axis off
MaxRecursionLevel = numel(S);
for level=1:MaxRecursionLevel
hp=plot(S(level).LineSeg,'k');
axis equal
axis(BBox);
saveas(gcf,[mfilename '_' sprintf('%03d',level)],'png');
saveas(gcf,[mfilename '_' sprintf('%03d',level)],'jpg');
plot2svg([mfilename '_' sprintf('%03d',level) '.svg']);
pause(0.5);
delete(hp);
end
plot(S(end).LineSeg,'k');
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function BBox = determineBoundingBox(S,proportionalOffset)
if nargin==1
proportionalOffset = 0.1;
end
BBox = zeros(1,4);
BBox(1) = min(real(S(end).LineSeg));
BBox(2) = max(real(S(end).LineSeg));
BBox(3) = min(imag(S(end).LineSeg));
BBox(4) = max(imag(S(end).LineSeg));
dBBoxX = BBox(2)-BBox(1);
dBBoxY = BBox(4)-BBox(3);
BBox = BBox + proportionalOffset * [-dBBoxX dBBoxX -dBBoxY dBBoxY];
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plot_Convergence_Evolution(S)
figure
hold on
box on
title('Evolution of the length of the curve with the number of levels');
xlabel('Level');
ylabel('Log of the length');
MaxRecursionLevel = numel(S);
lengthCurve = zeros(1,MaxRecursionLevel);
for level=1:MaxRecursionLevel
lengthCurve(level) = sum(abs(diff(S(level).LineSeg)));
end
plot(log2(lengthCurve));
grid on
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function cmd = generateGIFAnimationCommand(MaxRecursionLevel)
cmd = '!convert -antialias -density 100 -delay 60 ';
for level =[1:1:MaxRecursionLevel MaxRecursionLevel-1:-1:1]
cmd = [cmd mfilename '_' sprintf('%03d',level) '.png '];
end
cmd = [cmd mfilename '.gif'];
return;