Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

---

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Distribuzione triangolare
Funzione di densità di probabilità
Funzione di ripartizione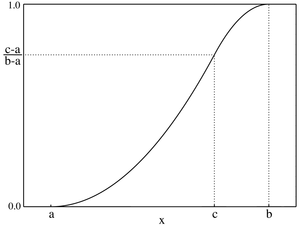
Parametri	${\displaystyle [a,b]\subset \mathbb {R} }$ ${\displaystyle c\in [a,b]}$
Supporto	${\displaystyle [a,b]}$
Funzione di densità	${\displaystyle {\begin{cases}{\frac {2}{b-a}}{\frac {x-a}{c-a}}&{\text{se }}a\leqslant x<c\\{\frac {2}{b-a}}&{\text{se }}x=c\\{\frac {2}{b-a}}{\frac {b-x}{b-c}}&{\text{se }}c<x\leqslant b\end{cases}}}$
Funzione di ripartizione	${\displaystyle {\begin{cases}{\frac {1}{b-a}}{\frac {(x-a)^{2}}{c-a}}&{\text{se }}a\leqslant x<c\\{\frac {c-a}{b-a}}&{\text{se }}x=c\\1-{\frac {1}{b-a}}{\frac {(b-x)^{2}}{b-c}}&{\text{se }}c<x\leqslant b\end{cases}}}$
Valore atteso	${\displaystyle {\frac {a+b+c}{3}}}$
Mediana	${\displaystyle a+{\sqrt {(b-a)(c-a)/2}}}$ se ${\displaystyle c\geqslant {\tfrac {a+b}{2}}}$ ${\displaystyle b-{\sqrt {(b-a)(b-c)/2}}}$ se ${\displaystyle c\leqslant {\tfrac {a+b}{2}}}$
Moda	${\displaystyle c\ }$
Varianza	${\displaystyle {\frac {(a^{2}+b^{2}+c^{2})-(ab+ac+bc)}{18}}}$
Indice di asimmetria	${\displaystyle {\frac {{\sqrt {2}}(a+b-2c)(2a-b-c)(a-2b+c)}{5(a^{2}+b^{2}+c^{2}-ab-ac-bc)^{\frac {3}{2}}}}}$
Curtosi	${\displaystyle -{\frac {3}{5}}}$
Entropia	${\displaystyle {\frac {1}{2}}+\log {\frac {b-a}{2}}}$
Funzione generatrice dei momenti	${\displaystyle 2{\frac {(b-c)e^{at}-(b-a)e^{ct}+(c-a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}$
Funzione caratteristica	${\displaystyle 2{\frac {(b-c)e^{iat}-(b-a)e^{ict}+(c-a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}$
Manuale

In teoria delle probabilità la distribuzione triangolare è una distribuzione di probabilità continua la cui funzione di densità di probabilità descrive un triangolo, ovvero che è nulla sui due valori estremi ed è lineare tra questi ed un valore intermedio (la moda).

In statistica viene utilizzata come modello quando il campione a disposizione è molto ristretto, stimando il minimo, il massimo e la moda.

La distribuzione triangolare con supporto ${\displaystyle [a,b]}$ e moda ${\displaystyle c}$ ha densità di probabilità

${\displaystyle f(x)={\begin{cases}{\frac {2}{b-a}}{\frac {x-a}{c-a}}&{\text{se }}a\leqslant x<c\\{\frac {2}{b-a}}&{\text{se }}x=c\\{\frac {2}{b-a}}{\frac {b-x}{b-c}}&{\text{se }}c<x\leqslant b\end{cases}}}$

Si possono considerare distribuzioni triangolari anche quelle distribuzioni per le quali la moda coincide con il valore minimo o massimo.

Quando la moda viene presa pari al punto medio ${\displaystyle {\tfrac {a+b}{2}}}$ dell'intervallo ${\displaystyle [a,b]}$, la distribuzione triangolare è simmetrica e viene anche detta distribuzione di Simpson, dal nome del matematico britannico Thomas Simpson.

Si può considerare anche una versione discreta della distribuzione triangolare, definendone la funzione di probabilità in modo lineare tra gli estremi e un valore intermedio.

Prese due variabili aleatorie indipendenti X e Y aventi entrambe distribuzione continua uniforme sull'intervallo unitario ${\displaystyle [0,1]}$, la distribuzione triangolare di parametri (a,c,b) descrive:

• per (0,1,2) la somma X+Y;
• per (-1,0,1) la differenza X-Y;
• per (0,0,1) la differenza in valore assoluto |X-Y|.

Nell'inferenza bayesiana se il parametro di una distribuzione di Bernoulli segue a priori la distribuzione uniforme sull'intervallo unitario, allora a posteriori delle osservazioni "fallimento" o "successo" il parametro segue una distribuzione triangolare con parametri (0,0,1) o (0,1,1) rispettivamente.

• Wikimedia Commons contiene immagini o altri file su distribuzione triangolare

• (EN) Eric W. Weisstein, Distribuzione triangolare, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Teknopedia che trattano di matematica