Voce principale: Leggi di Keplero.

Le leggi di Keplero che descrivono le proprietà delle orbite di oggetti sottoposti alla forza gravitazionale generata da un corpo massivo possono essere dedotte teoricamente applicando i principi della dinamica (equazioni di Newton).

Nel procedimento esposto, si dimostrerà inizialmente l'esistenza di un integrale primo del moto, la velocità areolare (seconda legge di Keplero); successivamente si proverà che le traiettorie nello spazio delle coordinate del sistema sono ellittiche (prima legge) e infine si troverà la dipendenza del periodo dell'orbita dalla lunghezza del semiasse maggiore dell'ellisse (terza legge).

Per la derivazione delle leggi di Keplero a partire dalle equazioni newtoniane e dalla legge di gravitazione universale è necessario innanzitutto introdurre un'approssimazione.

Ci limiteremo al caso in cui la massa del pianeta sia trascurabile rispetto a quella del Sole; in questo caso possiamo fissare il centro del sistema di riferimento nel centro del Sole e trascurarne il moto.

In quest'approssimazione, il problema di Keplero si riduce a quello di un moto in campo centrale in cui vale l'equazione di Newton

${\displaystyle m{\ddot {r}}=-{\frac {\partial V}{\partial r}}}$

dove ${\displaystyle V(r)=-k/r}$

Tale relazione si ottiene appunto integrando su ${\displaystyle r}$ l'espressione della forza gravitazionale ${\displaystyle F(r)=-k/r^{2}}$.

La seconda legge di Keplero afferma che la velocità areolare è costante durante il moto.

Ora, introducendo un sistema di coordinate polari ${\displaystyle (r,\theta )}$, con i rispettivi versori${\displaystyle (\mathbf {\hat {r}} ,\mathbf {\hat {\theta }} )}$ si ha, banalmente ${\displaystyle \mathbf {r} =r\mathbf {\hat {r}} }$.

Derivando tale quantità rispetto al tempo, si ottiene (applicando la regola della derivazione del prodotto e ricordando

${\displaystyle \mathbf {\dot {\hat {r}}} ={\dot {\theta }}\mathbf {\hat {\theta }} }$, ${\displaystyle \mathbf {\dot {\hat {\theta }}} =-{\dot {\theta }}\mathbf {\hat {r}} }$

${\displaystyle \mathbf {\dot {r}} ={\dot {r}}\mathbf {\hat {r}} +r{\dot {\theta }}\mathbf {\hat {\theta }} }$

Ora, considerando per semplicità la massa unitaria, il momento angolare ${\displaystyle \mathbf {L} }$ vale (sfruttando le proprietà del prodotto vettoriale):

${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {\dot {r}} =\mathbf {r} \times {\dot {r}}\mathbf {\hat {r}} +\mathbf {r} \times r{\dot {\theta }}\mathbf {\hat {\theta }} =r{\dot {\theta }}(\mathbf {r} \times \mathbf {\hat {\theta }} )=r^{2}{\dot {\theta }}(\mathbf {\hat {r}} \times \mathbf {\hat {\theta }} )=r^{2}{\dot {\theta }}}$

Diretto ortogonalmente al piano in cui si svolge il moto.

Per la legge di conservazione del momento angolare, segue che la quantità ${\displaystyle r^{2}{\dot {\theta }}}$ è un integrale del moto.

Considerando la velocità areolare ${\displaystyle C}$ come derivata temporale dell'area spazzata dal raggio vettore, si ha

${\displaystyle \mathrm {d} S={\frac {1}{2}}r^{2}{\dot {\theta }}\mathrm {d} t}$

Infatti, considerando un angolo ${\displaystyle \mathrm {d} \theta ={\dot {\theta }}\mathrm {d} t}$, l'area spazzata nell'intervallo temporale infinitesimo, l'elemento d'area è data dalla metà del quadrato di ${\displaystyle r}$ per l'angolo al centro.

Eseguendo la derivata:

${\displaystyle C={\frac {\mathrm {d} S}{\mathrm {d} t}}={\frac {1}{2}}r^{2}{\dot {\theta }}={\frac {1}{2}}L}$.

Pertanto la velocità areolare è un integrale del moto.^[1]

Si può notare come la validità della seconda legge sia del tutto indipendente dall'espressione del potenziale considerato, essa infatti è una proprietà di tutti i potenziali centrali.

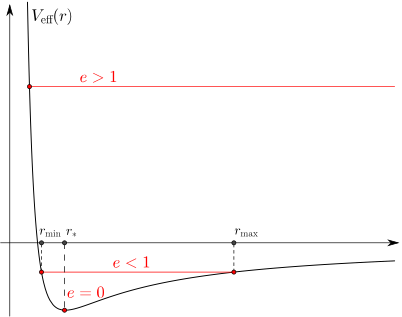
Innanzitutto il problema bidimensionale del moto in campo centrale può essere facilmente ridotto a un caso unidimensionale utilizzando la definizione del potenziale efficace.

Le equazioni del moto, infatti, possono essere riscritte considerando la forma

${\displaystyle V_{\text{eff}}={\frac {L^{2}}{2r^{2}}}+V(r)={\frac {L^{2}}{2r^{2}}}-{\frac {k}{r}}}$

In un moto in campo centrale, la relazione tra l'angolo ${\displaystyle \theta }$ e la distanza dall'origine ${\displaystyle r}$ è data dall'integrale

${\displaystyle \theta =\int {\frac {L/r^{2}\,\mathrm {d} r}{\sqrt {2(E-V_{\text{eff}}(r))}}}=\int {\frac {L/r^{2}\,\mathrm {d} r}{\sqrt {2(E-V_{\text{eff}}(r))}}}=\arccos {\frac {L/r-k/L}{\sqrt {(2E+k^{2}/L^{2})}}}}$

dove la costante integrativa è stata posta uguale a zero. Ciò significa che l'integrale viene calcolato a partire dal pericentro dell'orbita.

Definendo ora le quantità

${\displaystyle p=L^{2}/k,\qquad e={\sqrt {1+2EL^{2}/k^{2}}}}$

e invertendo opportunamente l'espressione di ${\displaystyle \theta }$ si giunge all'equazione

${\displaystyle r={\frac {p}{1+e\cos \theta }}}$.

Questa altro non è che l'espressione di una qualunque conica in coordinate polari centrata in un fuoco.

Se ${\displaystyle e<1,}$ questa rappresenta un'ellisse con eccentricità ${\displaystyle e}$ e semilato retto ${\displaystyle p}$.

In particolare, è possibile ottenere i valori dei semiassi ${\displaystyle a}$ e ${\displaystyle b}$:

${\displaystyle a={\frac {p}{1-e^{2}}}={\frac {L^{2}/k}{1-1-2EL^{2}/k^{2}}}={\frac {k}{2|E|}}}$

${\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}={\frac {L^{2}/k}{\sqrt {1-1-2EL^{2}/k^{2}}}}={\frac {L}{\sqrt {2|E|}}}}$

Nelle espressioni di ${\displaystyle a}$ e ${\displaystyle b}$ appena ricavate, si può notare come il semiasse maggiore ${\displaystyle a}$ sia dipendente solo dall'energia totale del sistema, mentre il semiasse minore sia anche funzione del momento angolare. Poiché il periodo di rotazione, nel moto in campo centrale, è funzione della sola energia, questo fatto permette di inferire per il periodo una relazione solo riguardante il semiasse maggiore dell'ellisse.

In particolare, si avrà (essendo ${\displaystyle \pi ab}$ l'area dell'ellisse e ${\displaystyle C}$ la velocità areolare, il cui valore è costante e uguale a ${\displaystyle L/2}$).

${\displaystyle T(E)={\frac {\pi ab}{C}}=\pi {\frac {k}{2|E|}}{\frac {L}{\sqrt {2|E|}}}{\frac {2}{L}}={\frac {\pi k}{\sqrt {2}}}|E|^{-3/2}}$

Ora, recuperando l'espressione di ${\displaystyle a}$ in funzione dell'energia si ha ${\displaystyle |E|={\frac {k}{2a}}}$, sostituendo tale valore nell'equazione precedente si ottiene

${\displaystyle T(E)={\frac {\pi k}{\sqrt {2}}}\left({\frac {2a}{k}}\right)^{3/2}}$

da cui si deduce che ${\displaystyle T^{2}\propto a^{3}}$ come afferma appunto la terza legge di Keplero.^[1]

Portale Meccanica: accedi alle voci di Teknopedia che trattano di Meccanica