Nell'ambito dei fenomeni di trasporto, la viscosità è il coefficiente di scambio di quantità di moto.^{[N 1]} Dal punto di vista microscopico la viscosità è legata all'attrito tra le molecole del fluido. Quando il fluido è fatto scorrere dentro una tubatura, le particelle che compongono il fluido generalmente si muovono più velocemente sull'asse della tubatura e più lentamente vicino alle sue pareti; per questa ragione uno sforzo, che si traduce in una differenza di pressione, è necessario per contrastare l'attrito tra gli strati di particelle e mettere in movimento il fluido. Lo sforzo percepito dal fluido è proporzionale alla sua viscosità.

La viscosità viene solitamente indicata con la lettera greca μ (mu o mi) o più raramente con la lettera η (eta) per richiamare il collegamento con il coefficiente di attrito della meccanica classica. Viene detta spesso "viscosità dinamica" per distinguerla dalla "viscosità cinematica", che è una grandezza legata alla viscosità dinamica ma dimensionalmente differente. Si definisce inoltre "fluidità" la grandezza reciproca della viscosità.^[1][2]

Un fluido che non ha viscosità si dice ideale. In realtà esistono a bassa temperatura dei fluidi senza viscosità, i cosiddetti superfluidi. Nel linguaggio comune spesso il limite di demarcazione tra i liquidi è posto dall'acqua, per cui si identificano per non viscosi i fluidi con viscosità minore dell'acqua. Inoltre fluidi con viscosità molto alta come la pece appaiono non molto diversi da un solido.

La parola viscosità deriva dal latino viscum (vischio): una pianta cespugliosa. Nell'antichità, dal succo delle bacche del vischio venivano preparate colle viscose.

Lo stesso argomento in dettaglio: Fluido newtoniano e Fluido non newtoniano.

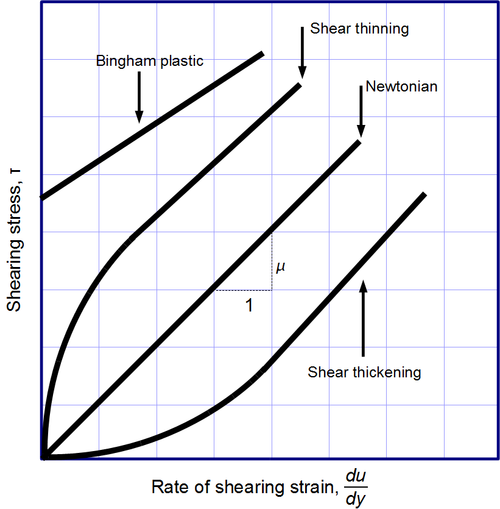
La legge di Stokes (viscosità lineare), analogamente ad altre leggi come la legge di Hooke, non è una legge fondamentale della natura, ma una legge che approssima il comportamento solo di alcuni materiali.

Tale legge definisce un comportamento viscoso ideale, caratterizzato da un valore del coefficiente di viscosità indipendente dallo sforzo di taglio ${\displaystyle \tau }$ e dal gradiente del flusso di scorrimento: i fluidi che obbediscono a tale legge sono detti fluidi newtoniani. In realtà per molti fluidi il coefficiente di viscosità ${\displaystyle \mu }$ è variabile con ${\displaystyle \tau }$. Un fluido caratterizzato da una risposta nel gradiente del flusso di scorrimento non lineare rispetto allo sforzo di taglio si denomina fluido non newtoniano. I gas, l'acqua e molti fluidi comuni sono in condizioni normali newtoniani. Per quanto riguarda i fluidi non newtoniani possiamo fare la seguente classificazione anche se non completa:

• pseudoplastici o plastiche di Bingham: fluidi che cominciano a deformarsi al di sopra di una certa soglia dello sforzo di taglio; al di sopra del valore di soglia, la velocità di deformazione ${\displaystyle {\frac {\partial u}{\partial y}}}$ diventa proporzionale allo sforzo di taglio come nei fluidi newtoniani.
• dilatante è un materiale che all'aumentare dello sforzo di taglio aumenta la sua viscosità; viene anche detto ispessente al taglio.
• assottigliante è un materiale che all'aumentare dello sforzo di taglio diminuisce la sua viscosità; viene anche detto assottigliante al taglio.
• tissotropici sono fluidi che diventano meno viscosi se vengono agitati o in qualche maniera messi in movimento.
• reopettici sono fluidi che diventano più viscosi se vengono agitati o in qualche maniera messi in movimento.

Nei fluidi newtoniani la viscosità è una funzione della loro composizione e temperatura. Nei gas e nei fluidi compressibili la viscosità dipende fortemente dalla temperatura e debolmente dalla pressione.

La viscosità di alcuni fluidi può dipendere da altri fattori. I fluidi magnetoreologici, per esempio, diventano più viscosi quando sono immersi in un campo magnetico, fino a comportarsi come un solido se il campo è molto intenso.

Un fluido con viscosità nulla ${\displaystyle (\mu =0)}$ e con densità costante al variare della pressione, quindi non viscoso e incomprimibile, si chiama fluido ideale. Un fluido la cui viscosità è trascurabile può essere definito anche inviscido. Quando la viscosità è pari a 0 si parla di superfluidità: tale caratteristica è propria per esempio di due isotopi dell'elio: nel ⁴He al di sotto dei 2,17 K, mentre per il ³He a una temperatura di 2,4 mK.

La viscosità di un fluido è determinata dal meccanismo con cui le molecole che lo compongono interagiscono tra di loro. Non vi è un'espressione semplice per la viscosità di un fluido. Le formule di Green-Kubo sono le più semplici ed esatte relazioni che permettono di determinare i coefficienti di trasporto, tra cui la viscosità, mediante degli integrali della funzione di correlazione temporale.^[3] Sebbene tali soluzioni siano esatte, per il calcolo della viscosità dei fluidi densi è necessario utilizzare tecniche di dinamica molecolare.^[3]
Vi è da aggiungere che determinare la viscosità dei gas rarefatti risulta un problema relativamente semplice. In tal caso, anche facendo delle semplici ipotesi basate sulla teoria cinetica dei gas, è possibile avere una buona comprensione dell'origine molecolare della viscosità. Una trattazione più sofisticata può essere sviluppata basandosi, con una opportuna divisione spaziale, sulla teoria di Chapman ed Enskog che utilizza l'equazione di Boltzmann per le molecole di gas.

La viscosità dinamica di un fluido è una misura della sua resistenza a fluire quando è applicato uno sforzo tangenziale. La causa di tale resistenza è dovuta agli strati adiacenti di fluido che si muovono con velocità diversa. La definizione viene data nel caso di regime laminare. La situazione ideale è quella di avere un fluido omogeneo, come in figura, tra due superfici piane orizzontali eguali, una fissa e l'altra mobile. Se la velocità del piano mobile è piccola e inoltre le particelle di fluido si muovono in direzione parallela al piano mobile con una velocità che varia linearmente da zero sul piano fisso a u sul piano mobile, in questo caso la viscosità dinamica è semplicemente data da:

${\displaystyle \mu ={\frac {Fd}{Su}}=\tau {\frac {d}{u}}}$

dove:

• ${\displaystyle F}$ è la forza che viene applicata al piano mobile
• ${\displaystyle d}$ è la distanza tra i due piani
• ${\displaystyle u}$ è la velocità costante del piano mobile
• ${\displaystyle S}$ è la superficie di ogni piano
• ${\displaystyle \tau ={\frac {F}{S}}}$ è lo sforzo di taglio

Nel caso più generale (come nella figura a fianco) la velocità del fluido non è una funzione lineare della distanza dal piano fisso, in questo caso la relazione tra sforzo di taglio e viscosità diventa:

${\displaystyle \mu =\tau {\frac {\partial y}{\partial u}}}$

dove adesso:

• ${\displaystyle y}$ è la distanza dal piano fisso dello strato di fluido generico
• ${\displaystyle u(y)}$ è la velocità locale del fluido.

Ogni strato si muoverà più velocemente dello strato sottostante. L'attrito tra di loro è la forza che impedisce il moto relativo dei due piani. Quindi il fluido eserciterà una forza sul piano superiore in direzione opposta al suo moto, e una forza eguale e opposta sul piano inferiore. Quindi lo sforzo tangenziale è necessario proprio per garantire una velocità uniforme del piano superiore. Per potere trascurare effetti di bordo, come implicitamente fatto, le dimensioni dei due piani devono essere molto maggiori della loro distanza.

In base alla sua definizione matematica la viscosità è dimensionalmente espressa da una forza su una superficie per un tempo, ovvero da una pressione per un tempo e, in termini di grandezze fondamentali, da ${\displaystyle \left[M\right]\left[L\right]^{-1}\left[T\right]^{-1}}$ (massa diviso lunghezza e tempo).

Spesso l'equazione precedente viene invertita e scritta:

${\displaystyle \tau =\mu {\frac {\partial u}{\partial y}}\qquad (1)}$

Si chiama in questa maniera il rapporto tra la viscosità dinamica di un fluido e la sua densità,^[4]:

${\displaystyle \nu ={\frac {\mu }{\rho }}}$

Spesso viene anche chiamata diffusività cinematica, essa è una misura della resistenza a scorrere di una corrente fluida sotto l'influenza della gravità. Questa tendenza dipende sia dalla viscosità dinamica sia dal peso specifico del fluido. Quando due fluidi di uguale volume sono messi in viscosimetri capillari identici e lasciati scorrere per gravità, il fluido avente maggior diffusività impiega più tempo a scorrere. Per esempio il mercurio risulta avere una viscosità dinamica 1,7 volte maggiore di quella dell'acqua, ma a causa del suo elevato peso specifico, esso percola molto più rapidamente da uno stesso foro a parità di volume. Infatti la viscosità cinematica del mercurio è nove volte minore di quella dell'acqua a temperatura ambiente (20 °C).^[5]

La viscosità cinematica è un parametro utile quando si ha a che fare con il numero di Reynolds, utile nello studio della fluido dinamica per distinguere tra regime laminare e regime turbolento. Il numero di Reynolds è dato in condizioni dinamiche dal rapporto tra le forze d'inerzia e le forze viscose:

${\displaystyle \mathrm {Re} ={\frac {\rho uL}{\mu }}={\frac {uL}{\nu }},}$

dove ${\displaystyle L}$ è tipica dimensione lineare nel sistema.

Lo stesso argomento in dettaglio: Viscosità di volume.

Quando un fluido compressibile è o compresso o espanso, senza sforzo di taglio, esso può anche in questo caso avere una forma di viscosità interna che rappresenta una resistenza alla deformazione. Queste forze sono collegate alla velocità di compressione o di espansione; per questa ragione si introduce un parametro in genere indicato con la lettera ${\displaystyle \lambda }$ che ha le dimensioni della viscosità dinamica. La viscosità di volume interviene nelle equazioni di Navier-Stokes che descrivono la dinamica dei fluidi. La viscosità di volume è importante solo quando il fluido è rapidamente compresso o espanso, come nel caso del suono o delle onde d'urto. La viscosità di volume spiega la perdita di energia di questo tipo di onde come descritto dalla legge di Stokes sull'attenuazione del suono.

Lo stesso argomento in dettaglio: Viscosimetro.

La viscosità è misurata con vari tipi di viscosimetri e reometri. Un reometro è usato per i fluidi non omogenei per i quali non è possibile dare un semplice valore della viscosità e perciò richiedono la misura di un numero maggiore di parametri rispetto a un viscosimetro. Poiché la viscosità dipende fortemente dalla temperatura, per fare una misura accurata occorre che la temperatura sia controllata con precisione: in particolare per materiali come i lubrificanti una variazione di temperatura di solo 5 °C può comportare un raddoppio della viscosità.

Per i fluidi newtoniani la viscosità è costante per un largo intervallo di sforzo tangenziale e quindi la viscosità è descritta da un singolo numero. Al contrario per i fluidi non newtoniani la viscosità è una funzione dello sforzo tangenziale applicato e in alcuni casi può dipendere anche dalla velocità con cui lo sforzo viene applicato.

Uno dei più comuni strumenti per misurare la viscosità cinematica è il viscosimetro a capillare di vetro.

Esistono anche viscosimetri che sfruttano diversamente le caratteristiche dei fluidi per misurare la viscosità. Per esempio un viscosimetro a coppa (utilizzato per le vernici) è composto da un contenitore graduato con un foro calibrato sul fondo. Più il fluido è viscoso, più tempo impiegherà a fluire attraverso il buco. Misurando il tempo di svuotamento della coppa è possibile (tramite opportune tabelle) risalire alla viscosità del fluido^[6].

Un altro tipo di viscosimetro è basato sulla misura del momento torcente. In questo caso si pone il fluido tra due piattelli, posti a una distanza regolabile. Uno dei due piattelli viene mantenuto fisso mentre l'altro viene fatto ruotare. In questo modo invece di una forza si misura il momento meccanico applicato e la velocità angolare del piatto mobile.

La misura della viscosità è ritenuta dagli addetti ai lavori come molto soggettiva, in quanto lo strumento di misura non riesce ad applicare correttamente la definizione della grandezza (una per tutte: usare un piattello, per esempio di acciaio, introduce uno strato di fluido in prossimità di esso che non si comporta come fluido libero e questo influenza la misura).

Normalmente, infatti, accanto a ogni misura di viscosità, occorre indicare in che condizioni e con quale strumento (inclusi marca e modello) è stata realizzata.

La viscosità dinamica si misura nel Sistema Internazionale in poiseuille (simbolo ${\displaystyle \mathrm {Pl} }$) e nel sistema cgs in poise (simbolo ${\displaystyle \mathrm {P} }$) vengono date le conversioni:

• ${\displaystyle 1\,\mathrm {Pa} \,s=1\,\mathrm {Pl} }$
• ${\displaystyle 1\,\mathrm {P} =0,1\,\mathrm {Pl} }$
• ${\displaystyle 1\,\mathrm {cP} =1\,m\mathrm {Pl} }$.

Il millipoiseuille (o centipoise) continua comunque a essere molto utilizzato in quanto esprime approssimativamente la viscosità dinamica dell'acqua a temperatura ambiente ${\displaystyle (1,001\,m\mathrm {Pl} }$ a ${\displaystyle 20^{\circ }\mathrm {C} }$).

Nel Sistema Internazionale la viscosità cinematica, avendo le dimensioni di una costante di diffusione cioè di una lunghezza al quadrato diviso un tempo, si misura in m²/s.

Nel sistema cgs l'unità di misura ${\displaystyle (cm^{2}/s)}$ prende il nome stokes e viene indicata con il simbolo ${\displaystyle \mathrm {St} }$. Si usa a volte un suo sottomultiplo il centistokes ${\displaystyle (\mathrm {cSt} )}$. Altre comuni, ma obsolete, unità di misura della viscosità cinematica sono il Saybolt Universal Seconds (SUS), Saybolt Furol Seconds (SFS).

${\displaystyle 1\,\mathrm {St} =1\,cm^{2}\cdot s^{-1}=10^{-4}m^{2}\cdot s^{-1}}$.

${\displaystyle 1\,\mathrm {cSt} =1\,mm^{2}\cdot s^{-1}=10^{-6}m^{2}\cdot s^{-1}}$.

L'acqua a 20 °C ha una viscosità cinematica di circa ${\displaystyle 10^{-6}m^{2}\cdot s^{-1}}$ o, in alternativa, ${\displaystyle 1\,\mathrm {cSt} }$.

La viscosità dei gas deriva principalmente dalla diffusione molecolare che trasporta quantità di moto tra i vari strati che scorrono. La teoria cinetica dei gas permette di fare previsione precise sulla viscosità dei gas se vengono rispettate le seguenti condizioni:

• La viscosità è indipendente dalla pressione
• La viscosità cresce all'aumentare della temperatura^[7]

Si deve a Maxwell nel 1866 lo studio del legame tra viscosità e teoria cinetica dei gas ^[8]. Per capire la ragione per cui la viscosità è indipendente dalla pressione si considerino due strati adiacenti (${\displaystyle A}$ e ${\displaystyle B}$) che si muovono l'uno rispetto all'altro. La viscosità del gas è determinata dalla probabilità che una particella dello strato ${\displaystyle A}$ entri nello strato ${\displaystyle B}$ trasferendo quantità di moto. Il calcolo di Maxwell dimostra che l'attrito interno è proporzionale alla densità e al cammino libero medio, che è inversamente proporzionale alla densità. Di conseguenza un aumento di densità dovuto a un aumento di pressione non determina una variazione della viscosità.

Consideriamo il caso di molecole di un gas perfetto, tra due piani uno fisso e l'altro a distanza ${\displaystyle D}$, che si muove con velocità costante ${\displaystyle u}$. Le particelle di gas di ogni strato hanno una velocità media ${\displaystyle {\overline {u}}_{x}(y)}$ (molto più bassa della velocità quadratica media ${\displaystyle v_{T}}$ dovuta alla agitazione termica), con ${\displaystyle y}$ variabile da ${\displaystyle 0}$ e ${\displaystyle D}$. La velocità media cresce con la distanza dal piano fisso, per cui particelle che dallo strato ${\displaystyle y-dy}$ vanno allo strato ${\displaystyle y}$ trasportano quantità di moto e determinano una forza resistente nello strato superiore e una trascinante (eguale e contraria nello stato inferiore). Vi sono nel gas ${\displaystyle n}$ molecole per unità di volume. Il cammino libero medio (la distanza media che percorrono le molecole) in un gas perfetto è:

${\displaystyle \lambda ={\frac {1}{{\sqrt {2}}\pi d^{2}n}}}$

${\textstyle d}$ è il diametro di collisione che dipende dalle proprietà microscopiche del gas.

La componente media della quantità di moto trasportata nello strato superiore dallo strato inferiore (cioè a ${\displaystyle y+\lambda }$) è pari a:

${\displaystyle {\frac {1}{2}}nmv_{Tx}{\overline {u}}_{x}(y-\lambda )}$

Il termine ${\displaystyle 1/2}$ dipende dal fatto che metà delle molecole dello strato inferiore hanno velocità verso l'alto e metà verso il basso. Inoltre si ha che:

${\displaystyle v_{T}^{2}=v_{Tx}^{2}+v_{Ty}^{2}+v_{Tz}^{2}\,\,\,}$ anche ${\displaystyle \,\,\,v_{Tx}^{2}=v_{Ty}^{2}=v_{Tz}^{2}\rightarrow v_{Tx}={\frac {1}{3}}v_{T}}$

quindi vi è uno sforzo tangenziale frenante dato da:

${\displaystyle {\frac {1}{6}}nmv_{T}{\overline {u}}_{x}(y-\lambda )}$

Contemporaneamente vi una sforzo tangenziale trascinante dovuto allo strato superiore:

${\displaystyle {\frac {1}{6}}nmv_{T}{\overline {u}}_{x}(y+\lambda )}$

Quindi la differenza tra queste due quantità è proprio ${\textstyle \tau }$:

${\displaystyle \tau ={\frac {1}{6}}nmv_{T}[{\overline {u}}_{x}(y+\lambda )-{\overline {u}}_{x}(y-\lambda )]}$

Poiché ${\displaystyle \lambda }$ è piccola si può fare lo sviluppo di Taylor (trascurando i termini di ordine superiore e omettendo il simbolo di media su ${\displaystyle u_{x}}$):

${\displaystyle \tau \approx {\frac {1}{6}}nmv_{T}[u_{x}(y)+\lambda {\frac {\partial u_{x}}{\partial y}}-u_{x}(y)+\lambda {\frac {\partial u_{x}}{\partial y}}]={\frac {1}{3}}nmv_{T}\lambda {\frac {\partial u_{x}}{\partial y}}}$

Se viene confrontata con l'espressione (1) si ha che:

${\displaystyle \mu ={\frac {1}{3}}nmv_{T}\lambda }$

Sostituendo a ${\displaystyle \lambda }$ la sua espressione:

${\displaystyle \mu ={\frac {1}{3}}nmv_{T}{\frac {1}{{\sqrt {2}}\pi d^{2}n}}={\frac {1}{3}}mv_{T}{\frac {1}{{\sqrt {2}}\pi d^{2}}}}$

Nella teoria cinetica dei gas si ha che:

${\displaystyle v_{T}={\sqrt {3k_{B}T/m}}}$

quindi:

${\displaystyle \mu ={\sqrt {\frac {mk_{B}T}{6}}}{\frac {1}{\pi d^{2}}}\qquad (2)}$

Cioè nei gas perfetti la viscosità dipende solo dalla temperatura: la pressione non ha nessun effetto.

In realtà nei gas reali, anche se la dipendenza dalla pressione è trascurabile, la dipendenza della viscosità dalla temperatura ha una dipendenza dalla temperatura maggiore di quella della equazione (2) approssimativamente data da:

${\displaystyle \mu =\gamma T^{\alpha }}$

Per alcuni gas la tabella seguente ricavata dall'Handbook of Chemistry and Physics^[9], fornisce i valori di ${\displaystyle \gamma }$ e ${\displaystyle \alpha }$:

Gas	Viscosità ${\displaystyle \mu }$ ${\displaystyle (\mu \mathrm {Pa} \ s\ a\ 300\ \mathrm {K} )}$	${\displaystyle \gamma \ (\mu \mathrm {Pa} \ s)}$	${\displaystyle \alpha }$
Anidride carbonica	${\displaystyle 15}$	${\displaystyle 0,079}$	${\displaystyle 0,92}$
Argon	${\displaystyle 22,9}$	${\displaystyle 0,197}$	${\displaystyle 0,83}$
Aria	${\displaystyle 18,6}$	${\displaystyle 0,216}$	${\displaystyle 0,78}$
Elio	${\displaystyle 20}$	${\displaystyle 0,42}$	${\displaystyle 0,66}$
Etano	${\displaystyle 9,5}$	${\displaystyle 0,060}$	${\displaystyle 0,89}$
Kripton	${\displaystyle 25,6}$	${\displaystyle 0,157}$	${\displaystyle 0,89}$
Idrogeno	${\displaystyle 9}$	${\displaystyle 0,18}$	${\displaystyle 0,68}$
Metano	${\displaystyle 11,2}$	${\displaystyle 0,104}$	${\displaystyle 0,82}$
Neon	${\displaystyle 32,1}$	${\displaystyle 0,643}$	${\displaystyle 0,68}$
Ossigeno	${\displaystyle 20,8}$	${\displaystyle 0,199}$	${\displaystyle 0,81}$

Nei liquidi, al contrario dei gas, la forza di legame tra le molecole non è mai trascurabile e questo comporta una maggiore viscosità rispetto ai gas. La viscosità eccetto casi di alta pressione è abbastanza indipendente dalla pressione. Invece all'aumentare della temperatura la viscosità diminuisce. In ogni caso la viscosità dei liquidi è vari ordini di grandezza maggiore che nei gas.

Tabella della viscosità di alcuni liquidi:

Liquido	Viscosità ${\displaystyle (\mathrm {Pa} \ s}$ a ${\displaystyle 300\ \mathrm {K} )}$ (se non specificato)
Acetone	${\displaystyle 3,06\times 10^{-4}}$
Benzene	${\displaystyle 6,04\times 10^{-4}}$
Olio di ricino	${\displaystyle 0,985}$
Sciroppo di mais	${\displaystyle 1,3806}$
Alcol etilico	${\displaystyle 1,074\times 10^{-3}}$
Glicole etilenico	${\displaystyle 1,61\times 10^{-2}}$
Glicerina (a 20 °C)	${\displaystyle 1,2}$
Mercurio	${\displaystyle 1,53\times 10^{-3}}$
Alcol metilico	${\displaystyle 5,44\times 10^{-4}}$
Olio lubrificante SAE 10 (20 °C)	${\displaystyle 0,065}$
Olio lubrificante SAE 40 (20 °C)	${\displaystyle 0,319}$
Nitrobenzene	${\displaystyle 1,83\times 10^{-3}}$
Azoto liquido (−196 °C 77 K)	${\displaystyle 0,158}$
Propanolo	${\displaystyle 1,94\times 10^{-3}}$
Olio di oliva	${\displaystyle 0,081}$
Pece	${\displaystyle 2,3\times 10^{8}}$
Acido solforico	${\displaystyle 0,024}$
Acqua	${\displaystyle 8,94\times 10^{-4}}$

Lo stesso argomento in dettaglio: Olio lubrificante, Classificazione viscosimetrica degli oli lubrificanti e CentiStokes.

La tabella SAE J300 (Society of Automotive Engineers) classifica gli oli motore in base alla viscosità, e non tenendo conto di nessun'altra caratteristica del lubrificante.

Il primo numero della classificazione seguito dalla lettera ${\displaystyle \mathrm {W} }$ (Winter) e dal successivo numero, indicano l'intervallo di temperatura esterno per cui quel tipo di olio mantiene una soddisfacente viscosità cinematica.

Si definisce "monogrado" un olio che garantisce una sola prestazione, a freddo o a caldo, indicata nella tabella (per esempio SAE 10W, SAE 20W, SAE 30, SAE 50).

Si definisce "multigrado" un olio che garantisce sia una prestazione a bassa temperatura sia una ad alta temperatura (per esempio SAE 5W30, SAE 10W40, SAE 15W50).

La scelta della viscosità di un lubrificante va operata tenendo in considerazione sia la temperatura minima di funzionamento del motore (temperatura invernale) sia quella massima (temperatura estiva): è fondamentale scegliere un olio che resti sufficientemente fluido a bassa temperatura per garantire un facile avviamento, ma che allo stesso tempo assicuri un mantenimento soddisfacente della viscosità quando il motore è sotto sforzo.

Altre caratteristiche fondamentali del lubrificante (come resistenza meccanica, antischiuma o resistenza alla temperatura) sono invece stabilite dalle specifiche internazionali (API, ACEA, JASO).

Numero di Viscosità SAE	${\displaystyle -18^{\circ }\mathrm {C} ,\,\mathrm {Pl} }$		${\displaystyle 100^{\circ }\mathrm {C} ,\,\mathrm {cSt} }$		${\displaystyle \mathrm {BPT} }$
	min	max	min	max	${\displaystyle ^{\circ }\mathrm {C} }$
${\displaystyle 5\mathrm {W} }$	-	${\displaystyle 1,25}$	${\displaystyle 3,8}$	-	${\displaystyle -30}$
${\displaystyle 10\mathrm {W} }$	${\displaystyle 1,25}$	${\displaystyle 2,5}$	${\displaystyle 4,1}$	-	${\displaystyle -25}$
${\displaystyle 15\mathrm {W} }$	${\displaystyle 2,5}$	${\displaystyle 5,0}$	${\displaystyle 4,1}$	-	${\displaystyle -20}$
${\displaystyle 20\mathrm {W} }$	${\displaystyle 5,0}$	${\displaystyle 10,0}$	${\displaystyle 56}$	-	${\displaystyle -15}$
${\displaystyle 20}$	.	.	${\displaystyle 5,6}$	${\displaystyle 9,3}$	.
${\displaystyle 30}$	.	.	${\displaystyle 9,3}$	${\displaystyle 12,5}$	.
${\displaystyle 40}$	.	.	${\displaystyle 12,5}$	${\displaystyle 16,3}$	.
${\displaystyle 50}$	.	.	${\displaystyle 16,3}$	${\displaystyle 21,9}$	.

Le viscosità a ${\displaystyle -18^{\circ }\mathrm {C} }$ sono misurate in un viscosimetro rotazionale (cold cranking simulator), quelle a ${\displaystyle 100^{\circ }\mathrm {C} }$ in un viscosimetro a capillare. La sigla ${\displaystyle \mathrm {W} }$ sta per winter (inverno) e definisce la serie di oli invernali. ${\displaystyle \mathrm {BPT} }$ è la temperatura limite pompaggio.

Tale indice esprime la costanza della graduazione viscosa di un determinato olio alle diverse temperature, quindi tanto quanto questo valore sarà maggiore e tanto la viscosità rimarrà costante al variare della temperatura, mentre minore sarà tale valore e maggiore risulterà tale variazione^[10].

È comunemente accertato che i solidi amorfi, come il vetro, hanno viscosità, basandosi sul fatto che tutti i solidi fluiscono impercettibilmente in risposta a uno sforzo di taglio (in inglese shear stress). Il vetro può infatti essere interpretato come un fluido ad altissima viscosità (il vetro non ha un punto di fusione definito, non possedendo una struttura cristallina - vedi anche calore di fusione).

Alcuni sostengono che la distinzione tra solidi e liquidi non sia chiara e che i solidi siano semplicemente liquidi con un'alta viscosità, tipicamente maggiore di ${\displaystyle 10^{12}\,\mathrm {Pa} \cdot s}$. I sostenitori di questa posizione la giustificano spesso con l'affermazione (diffusa ma falsa) che il vetro può fluire in modo estremamente lento.

Un esempio a questo proposito è rappresentato dalle antiche vetrate decorative di chiese e altri edifici storici. Secoli fa, la lavorazione del vetro era un'attività quasi interamente manuale, quindi non sorprende affatto che ci siano delle irregolarità nelle sottili lastre colorate destinate a comporre le fini vetrate. Oggigiorno, i restauratori d’arte hanno notato che i singoli cocci di vetro che compongono la vetrata, presentano tutti una dilatazione alla loro base. Una parte sottile in alto e una parte più spessa in basso. Per spiegare questo nel tempo è sorta l’ipotesi che questo fenomeno sia causato dalle proprietà del vetro che, possedendo una viscosità non infinita, con il passare dei secoli e grazie alla gravità, sia “scivolato” come un liquido e si sia quindi accumulato alla base, formando un leggero rigonfiamento. Questa spiegazione, seppur sembri convincente e plausibile, non ha alcun fondamento di verità in quanto ci è noto che i mastri vetrai solevano disporre volutamente i cocci di vetro imperfetti con il lato pesante rivolto verso il basso, in modo da donare maggiore stabilità alla fragile vetrata.

La falsità dell’ipotesi di partenza è stata mostrata anche dal fatto che antichi telescopi, ancora più vecchi delle vetrate stesse, generano ancora oggi immagini perfettamente a fuoco, nonostante le loro delicate ottiche (lenti e specchi) in purissimo vetro, siano estremamente sensibili a piccole variazioni nell’allineamento. È noto anche che la viscosità del piombo, materiale che incornicia i vetri, è svariati ordini di grandezza più piccola di quella del vetro, quindi anche se il vetro fosse “scivolato” verso il basso anche solo di poco, il piombo avrebbe dovuto “sciogliersi” e praticamente trasformarsi in una pozzanghera ai piedi della vetrata.

Anche se molti solidi fluiscono, quando sottoposti a sforzi elevati, essi sono caratterizzati dal loro comportamento a basso sforzo. La viscosità può essere un'appropriata caratteristica dei solidi in regime plastico.

Questo uso del termine viscosità può generare confusione quando usato in relazione a certi materiali solidi, come i materiali di Maxwell, per descrivere la relazione tra sforzo e velocità di variazione della tensione piuttosto che della velocità di taglio.

Queste distinzioni possono essere in gran parte risolte considerando le equazioni costitutive del materiale in questione, che tengono conto del suo comportamento viscoso ed elastico.

I materiali che sono importanti per la loro viscosità ed elasticità, entro un particolare intervallo di valori di deformazione e di rapidità di deformazione, sono chiamati viscoelastici.

I materiali che esibiscono una deformazione viscosa almeno tre volte maggiore della loro deformazione elastica sono chiamati a volte reidi. Un esempio di solido che fluisce, che è stato osservato dal 1927, è la pece, usata per esempio nell'esperimento della goccia di pece, cioè un esperimento che misura il percolo di un pezzo di pece negli anni. La pece fluisce a temperatura ambiente sebbene molto lentamente.

Nell'ambito dell'ingegneria delle strutture si definisce con il termine scorrimento viscoso (in inglese creep e in francese fluage) il fenomeno per cui in una struttura realizzata in calcestruzzo, libera di deformarsi e in condizioni di carico esterno di compressione costante, dopo le deformazioni istantanee elastiche, sviluppa deformazioni differite nel tempo.

Tale fenomeno fa sì che la variabile "tempo" appaia nelle equazioni costitutive del materiale ed è dovuto al fatto che il calcestruzzo dal punto di vista reologico presenta un comportamento viscoelastico, cioè intermedio tra il comportamento elastico (proprio dei solidi) e del comportamento viscoso (proprio dei liquidi).

Per bassi valori di carico applicato e considerando un tempo di osservazione abbastanza breve (durante il quale permangono tali tensioni), il comportamento reologico del calcestruzzo può definirsi elastico lineare.

Dato un parallelepipedo di calcestruzzo, applicando su di esso una forza di compressione esso entrerà in tensione, e subirà un accorciamento istantaneo che è da attribuirsi alla componente elastica della viscosità (viscosità elongazionale, dall'inglese elongational viscosity). Se poi viene lasciata invariata nel tempo la forza sull'oggetto, senza rimuoverla né variarla d'intensità, lo stato tensionale rimarrà invariato, e avendo comportamento viscoso si potrà vedere invece che continueranno a registrarsi accorciamenti, ossia l'oggetto continua a deformarsi. Tali deformazioni sono legate alla componente puramente viscosa della viscosità (viscosità di taglio, dall'inglese shear viscosity). Se dopo avere avuto anche le deformazioni viscose si rimuove il carico si osserva che le deformazioni elastiche non verranno recuperate totalmente, poi nel tempo si vedrà anche il recupero di una parte delle deformazioni viscose. Questo parziale recupero delle deformazioni è dovuto all'irrigidimento del materiale nel corso del tempo in cui è stato sottoposto a carico. Si osserva così un materiale più resistente, rispetto al parallelepipedo iniziale.

La viscosità nel calcestruzzo è dovuta a vari fattori, tra cui:

• stato del conglomerato
  • caratteristiche meccaniche
  • livello di tensioni presenti
  • età del conglomerato all'atto della messa in carico
• ambiente di maturazione:
  • temperatura
  • umidità relativa
• geometria dell'elemento
  • superficie specifica a contatto con l'ambiente esterno.^{[N 2]}

Le normative di riferimento fanno dipendere le deformazioni viscose dal coefficiente di viscosità ${\displaystyle \Phi (t_{\infty },\,t_{o})}$ dipendente dai fattori di cui sopra.

Se lo stato di tensione del calcestruzzo all'istante ${\displaystyle t_{0}}$ di messa in carico risulta ${\displaystyle <45\%f_{ck}}$, l'Eurocodice 2 e il D.M. 14 gennaio 2008 propongono la teoria lineare della viscosità per la quale la deformazione viscosa è data dalla seguente relazione lineare:

• ${\displaystyle \varepsilon _{V}=\Phi (t_{\infty },\,t_{o})\varepsilon _{e}}$

dove:

• ${\displaystyle t_{o}}$ = età del calcestruzzo all'applicazione del carico
• ${\displaystyle \varepsilon _{e}}$ = deformazione istantanea elastica.

Annotazioni

Fonti

• (EN) Warren E Stewart e Edwin N Lightfoot, Transport phenomena, 2ª ed., New York, J. Wiley, 2007, ISBN 0-470-11539-4, OCLC 77079936.
• Paolo Silvestroni, Fondamenti di chimica, 10ª ed., Zanichelli; CEA, 1999, ISBN 88-408-0998-8, OCLC 799748493.
• Donato Spataro, Trattato teorico e pratico di idromeccanica. v.1-, Milano, U. Hoepli, 1915, pp. 78-165, OCLC 23517589.

• Legge di Newton (fluidodinamica)
• Legge di Poiseuille
• Melt Flow Index

• Wikizionario contiene il lemma di dizionario «viscosità»
• Wikimedia Commons contiene immagini o altri file sulla viscosità

• Viscosità, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Tommaso Collodi e Guido Vernoni, VISCOSITÀ, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1937.
• Viscosita, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
• Mauro Cappelli, Viscosita, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
• Viscosità, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• viscosità, su sapere.it, De Agostini.
• (EN) viscosity, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Opere riguardanti Viscosity, su Open Library, Internet Archive.
• Coefficienti di viscosità, su itchiavari.org.
• (EN) Creep Analysis Research Group - Politecnico di Torino, su polito.it. URL consultato il 14 gennaio 2007 (archiviato dall'url originale il 14 maggio 2016).
• (EN) Dimostrazione dell'alta viscosità della pece nera - Premio IG Nobel 2005, su physics.uq.edu.au.

Portale Fisica

Portale Ingegneria

Portale Meccanica